一种含干扰观测器的高超声速飞行器跟踪控制方法与流程
本发明涉及含干扰观测器的高超声速飞行器跟踪控制方法。
背景技术:
高超声速飞行器是指飞行速度大于5马赫的飞行器,其速度快、突防能力强,有着巨大的军事价值和经济价值(Dydek Z T,Annaswamy A M,Lavretsky E.Adaptive control and the NASA X-15-3flight revisited[J].Control Systems,IEEE,2010,30(3):32-48)。然而,由于其采用了发动机/机体的一体化设计,导致机体结构和推进系统之间的强耦合以及动力学系统具有复杂非线性特性(Bolender M A,Doman D B.Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle[J].Journal of Spacecraft and Rockets,2007,44(2):374-387)。另外由于飞行器巡航过程中的燃料消耗、气动热引起的机体形变等因素会使模型产生较大的不确定性(Sigthorsson D,Jankovsky P,Serrani A,et al.Robust linear output feedback control of an airbreathing hypersonic vehicle[J].Journal of Guidance,Control,and Dynamics,2008,31(4):1052-1066)。由上述可知,高超声速飞行器飞行包线大、飞行环境复杂,具有气动特性变化剧烈,模型不确定性强等特点。这些特点使得对其控制系统设计面临着巨大的挑战。
近年来各类非线性控制算法日渐成熟,并逐渐应用于高超声速飞行器的控制器设计中。文献(Watts A C.Control of a High Performance Maneuvering Reentry Vehicle Using Dynamic Inversion{C}[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.2005:1-16),(Mathavaraj S,Halbe O,Padhi R.Robust control of a reusable launch vehicle in reentry phase using model following neuro-adaptive design[C]//Proceedings of the AIAA Guidance,Navigation,and Control Conference.2010:2-5),(Parker J T,Serrani A,Yurkovich S,et al.Control-oriented modeling of an air-breathing hypersonic vehicle[J].Journal of Guidance,Control,and Dynamics,2007,30(3):856-869)利用系统的输出线性化方法对高超声速飞行器进行控制器设计。然而,基于动态逆或反馈线性化的方法要求高超声速飞行器模型具备反馈线性化的条件,而这在实际情况中通常无法满足,另外,当被控对象中有不确定性参数或者未建模动态存在时,不能保证其鲁棒性,需要与其他的鲁棒控制方法结合使用(Burken J J,Lu P,Wu Z L.Reconfigurable flight control designs with application to the X-33vehicle[C].AIAA Guidanee,Navigation,and Control Conference and Exhibit,AIAA1999-4134),(Bu X,Wu X,Ma Z,et al.Novel adaptive neural control of flexible air-breathing hypersonic vehicles based on sliding mode differentiator[J].Chinese Journal of Aeronautics,2015,28(4):1209-1216)。为了满足实际工程中对系统在有限时间内稳定的需求,有限时间控制方法相比于渐近稳定和指数稳定控制方法具有实际意义和理论价值。自文献(Zhu Z,Xia Y,Fu M.Attitude stabilization of rigid spacecraft with finite‐time convergence[J].International Journal of Robust and Nonlinear Control,2011,21(6):686-702),(Yu X,Man Z.Model reference adaptive control systems with terminal sliding modes[J].International Journal of Control,1996,64(6):1165-1176)提出了有限时间终端滑模控制理论以来,基于滑模的有限时间控制理论受到广泛关注。对于传统终端滑模控制中存在的控制奇异和远离平衡点时收敛缓慢的两个问题。为了解决终端滑模控制的奇异问题,文献(Feng Y,Yu X,Han F.On nonsingular terminal sliding-mode control of nonlinear systems[J].Automatica,2013,49(6):1715-1722)通过引入新型饱和函数避免了终端滑模控制器奇异问题。文献(Mu C,Sun C,Xu W.Fast sliding mode control on air-breathing hypersonic vehicles with transient response analysis[J].Proceedings of the Institution of Mechanical Engineers,Part I:Journal of Systems and Control Engineering,2016,230(1):23-34),(Feng Y,Yu X,Man Z.Non-singular terminal sliding mode control of rigid manipulators[J].Automatica,2002,38(12):2159-2167),(Yang L,Yang J.Nonsingular fast terminal sliding‐mode control for nonlinear dynamical systems[J].International Journal of Robust and Nonlinear Control,2011,21(16):1865-1879),(Xu S S D,Chen C C,Wu Z L.Study of nonsingular fast terminal sliding-mode fault-tolerant control[J].IEEE Transactions on Industrial Electronics,2015,62(6):3906-3913),(Xiaohu Z X W,Gongzhang Z J S.Disturbance compensated terminal sliding mode control for hypersonic vehicles[J].Journal of Beijing University of Aeronautics and Astronautics,2012,11:008)基于非奇异终端滑模理论,设计了非奇异终端滑模有限时间控制器。文献(Mu C,Sun C,Xu W.Fast sliding mode control on air-breathing hypersonic vehicles with transient response analysis[J].Proceedings of the Institution of Mechanical Engineers,Part I:Journal of Systems and Control Engineering,2016,230(1):23-34)通过引入辅助误差变量,将高超声速飞行器反馈线性化模型转化为多变量二阶模型,设计了非奇异终端滑模面,但控制器中含有符号函数项,会引起系统抖振。为了进一步提高当系统状态离平衡点较远时的收敛速率,文献(Xiaohu Z X W,Gongzhang Z J S.Disturbance compensated terminal sliding mode control for hypersonic vehicles[J].Journal of Beijing University of Aeronautics and Astronautics,2012,11:008)提出了改进型终端滑模面,在平衡点附近由非线性滑模面切换至高增益线性滑模面,不仅避免了奇异问题,且具有较高的收敛速率。
除了奇异问题,抖振现象是限制滑模控制理论在工程应用的关键因素。文献(Feng Y,Yu X,Man Z.Non-singular terminal sliding mode control of rigid manipulators[J].Automatica,2002,38(12):2159-2167)、(Sun H,Li S,Sun C.Finite time integral sliding mode control of hypersonic vehicles[J].Nonlinear Dynamics,2013,73(1-2):229-244)利用边界层技术,通过饱和函数代替符号函数来削弱系统抖振,但由于系统不确定性或外界扰动存在,在一定程度上降低了控制系统性能,会导致系统存在稳定误差,使稳态误差界求取具有一定保守性。在控制系统设计中加入观测器是一种更加主动和直接的处理系统扰动的方法(Li S,Sun H,Yang J,et al.Continuous finite-time output regulation for disturbed systems under mismatching condition[J].IEEE Transactions on Automatic Control,2015,60(1):277-282),(He S,Lin D,Wang J.Continuous second-order sliding mode based impact angle guidance law[J].Aerospace Science and Technology,2015,41:199-208),(Yang J,Li S,Su J,et al.Continuous nonsingular terminal sliding mode control for systems with mismatched disturbances[J].Automatica,2013,49(7):2287-2291),(Zong Q,Wang J,Tian B,et al.Quasi-continuous high-order sliding mode controller and observer design for flexible hypersonic vehicle[J].Aerospace Science and Technology,2013,27(1):127-137),(Wang F,Zou Q,Hua C,et al.Disturbance observer–based dynamic surface control design for a hypersonic vehicle with input constraints and uncertainty[J].Proceedings of the Institution of Mechanical Engineers,Part I:Journal of Systems and Control Engineering,2016,230(6):522-536),(Wu G,Meng X.Nonlinear disturbance observer based robust backstepping control for a flexible air-breathing hypersonic vehicle[J].Aerospace Science and Technology,2016,54:174-182),(Wang J H,Liu L H,Wang P,et al.Guidance and control system design for hypersonic vehicles in dive phase[J].Aerospace Science and Technology,2016,53:47-60),(Wang J,Wu Y,Dong X.Recursive terminal sliding mode control for hypersonic flight vehicle with sliding mode disturbance observer[J].Nonlinear Dynamics,2015,81(3):1489-1510),(Peng L,Xuefeng P,Jianjun M,et al.Non-homogeneous disturbance observer-based second order sliding mode control for a tailless aircraft[C]//Chinese Automation Congress(CAC),2013.IEEE,2013:120-125)。文献(Zong Q,Wang J,Tian B,et al.Quasi-continuous high-order sliding mode controller and observer design for flexible hypersonic vehicle[J].Aerospace Science and Technology,2013,27(1):127-137)基于高阶滑模观测器,利用终端滑模理论,设计了拟连续高阶滑模控制器,并验证了方法的有效性,由于滑模面包含积分部分,降低了系统瞬态性能。文献(Wang F,Zou Q,Hua C,et al.Disturbance observer–based dynamic surface control design for a hypersonic vehicle with input constraints and uncertainty[J].Proceedings of the Institution of Mechanical Engineers,Part I:Journal of Systems and Control Engineering,2016,230(6):522-536),(Wu G,Meng X.Nonlinear disturbance observer based robust backstepping control for a flexible air-breathing hypersonic vehicle[J].Aerospace Science and Technology,2016,54:174-182)提出基于反步法联合干扰观测器的高超声速飞行器控制器设计方法,利用干扰观测器估计系统未知干扰,提高了系统鲁棒性。文献(Wang J H,Liu L H,Wang P,et al.Guidance and control system design for hypersonic vehicles in dive phase[J].Aerospace Science and Technology,2016,53:47-60)提出了非奇异终端滑模控制方法,采用干扰观测器估计系统干扰,提高了系统抗扰动性能,降低了滑模控制器增益和削弱了系统抖振。文献(Wang J,Wu Y,Dong X.Recursive terminal sliding mode control for hypersonic flight vehicle with sliding mode disturbance observer[J].Nonlinear Dynamics,2015,81(3):1489-1510)在提出积分-微分滑模面的基础上,利用滑模干扰观测器估计系统外界干扰,设计了递推滑模控制器,但没有对整个闭环系统稳定性进行证明。
技术实现要素:
本发明是为了解决现有技术没有证明观测器在观测系统干扰过程中是有界的问题,而提出的一种含干扰观测器的高超声速飞行器跟踪控制方法。
一种含干扰观测器的高超声速飞行器跟踪控制方法以下步骤实现:
步骤一:根据高超声速飞行器纵向输入输出线性化模型,建立带有系统干扰的二阶系统模型;
步骤二:根据步骤一建立的带有系统干扰的二阶系统模型,基于滑模控制理论,设计有限时间终端滑模控制器;
步骤三:对步骤二设计的有限时间终端滑模控制器进行系统稳定性证明。
发明效果:
本发明基于有限时间滑模理论和NHDO设计了快速终端滑模有限时间跟踪控制器,使得系统滑模面是有限时间稳定的,系统状态是渐近收敛的。与以上文献相比,创新之处如下:
(1)本发明对整个闭环系统进行稳定性证明,可保证系统所有状态在NHDO的收敛阶段是有界的。
(2)本发明利用NHDO对系统总干扰进行估计,降低控制器增益,减弱了系统抖振,但没有牺牲系统的动态性能。与现有技术中滑模面相比,具有更快的收敛速率。
(3)本发明给出的带有系统干扰的二阶系统模型,便于控制器的设计。
附图说明
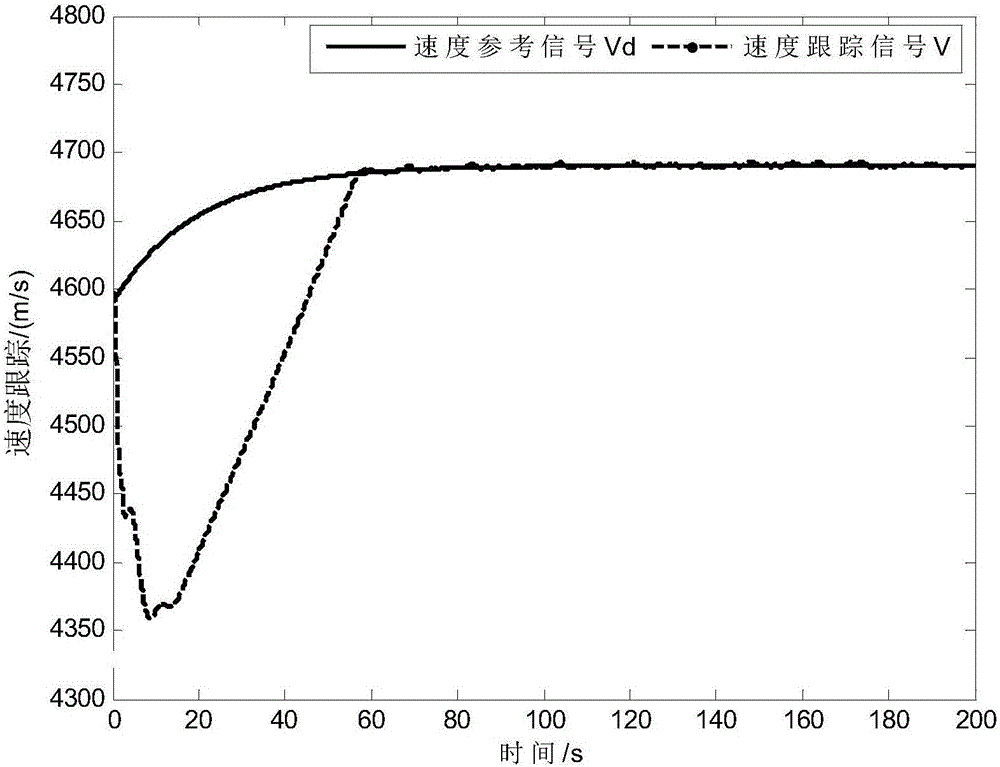
图1为速度参考指令跟踪曲线图;
图2为速度误差跟踪曲线图;
图3为高度参考指令跟踪曲线图;
图4为高度误差跟踪曲线图;
图5为控制输入φc,δe曲线图;
图6为攻角、俯仰角和俯仰角速率曲线图;
图7为自适应参数曲线图;
图8为系统总干扰估计曲线图;
图9为系统干扰估计误差曲线图。
具体实施方式
具体实施方式一:一种含干扰观测器的高超声速飞行器跟踪控制方法包括以下步骤:
首先,给出了高超声速飞行器纵向输入输出线性化模型,在此基础上,建立了带有系统干扰的二阶系统模型。其次,在提出快速非奇异终端滑模的基础上,基于NHDO对系统干扰进行有效估计,设计了有限时间终端滑模控制器,实现了高超声速飞行器的快速稳定跟踪控制。最后,利用李雅普诺夫稳定性理论对整个闭环系统稳定性给出了理论证明,保证系统状态在NHDO收敛阶段是有界的,并对高超声速纵向非线性模型进行数字仿真,进一步验证了所设计控制器的有效性。
步骤一:根据高超声速飞行器纵向输入输出线性化模型,建立带有系统干扰的二阶系统模型;
步骤二:根据步骤一建立的带有系统干扰的二阶系统模型,基于滑模控制理论,设计有限时间终端滑模控制器;
步骤三:对步骤二设计的有限时间终端滑模控制器进行系统稳定性证明。
具体实施方式二:本实施方式与具体实施方式一不同的是:所述步骤一中建立带有系统干扰的二阶系统模型具体过程为:
选取文献(Bolender M A,Doman D B.Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle[J].Journal of Spacecraft and Rockets,2007,44(2):374-387)中给出的美国国家航空航天局兰利研究中心提出的刚性高超声速飞行器模型如下:
其中V为飞行的速度,h为飞行高度,α为飞行攻角,θ为飞行俯仰角,q为俯仰角速率,φ为发动机节流阀和为节流阀的一阶导数;μ为地球引力常数,r=h+RE,RE为地球半径,γ=θ-α为航迹角,M为控制力矩,Iyy为转动惯量,g为重力加速度;相关力及力矩系数见文献(Zhu Z,Xia Y,Fu M.Attitude stabilization of rigid spacecraft with finite‐time convergence[J].International Journal of Robust and Nonlinear Control,2011,21(6):686-702)。
发动机的二阶动力学模型如下:
其中φ为发动机节流阀,φc为发动机节流阀设定的指令,ωn为发动机动力学的无阻尼自然频率,ζ为其阻尼比;
控制输入u选为[φc δe]T,φc为节流阀设定指令,δe为升降舵偏角指令,系统(1)输出y选为[V h]T;系统(1)为公式(1)。
为了便于高超声速飞行器控制系统的设计,采用输入输出线性化方法来处理模型,采用文献(Sun H,Li S,Sun C.Finite time integral sliding mode control of hypersonic vehicles[J].Nonlinear Dynamics,2013,73(1-2):229-244)线性化系统模型。系统(1)线性化模型:
其中,Δfv,Δfh,Δb11,Δb12,Δb21,Δb22是由参数不确定性和外界干扰产生的有界项。令dV=ΔfV+Δb11δe+Δb12φc,dh=Δfh+Δb21δe+Δb22φc;
为了克服对高阶系统设计控制器困难的问题,在定义跟踪误差变量基础上,引入辅助误差变量,其中,Vd(x)、hd(x)分别为期望输出速度、高度参考指令:
联合式(4)和式(3)整理成带有系统干扰的多变量二阶系统模型:
其中,
令则式(7)重新写为:
本发明控制目标:实现高超声速飞行器输出速度V和高度h能够快速稳定跟踪期望的速度指令Vd和高度指令hd,并同时保证攻角α、俯仰角θ、俯仰角速率q保持在一定的变化范围内。
相关引理及假设
定义若系统
其中f:U0→Rn是定义在ξ=0的开邻域U0上的一个连续函数。如果系统在平衡点ξ=0的邻域U∈U0内是李雅普诺夫稳定的,并且是有限时间稳定的,则系统(9)的平衡点是局部有限时间稳定的。如果f:U=Rn,则系统(9)的平衡点是全局有限时间稳定的。
针对系统(9),假设存在连续可微函数V,并且满足条件:
(1)V为正定函数。
(2)存在正实数c>0和α∈(0,1),以及一个包含原点的开邻域使得成立。
则系统是有限时间稳定的,并且收敛时间T满足其中V0为V的初始值,若U=U0=Rn,则系统为全局有限时间稳定的。
假设1.针对系统(8)干扰d存在且可微Lipschitz常数L=[L1,L2]T,即存在已知正常数L1和L2,分别满足和
其它步骤及参数与具体实施方式一相同。
具体实施方式三:本实施方式与具体实施方式一或二不同的是:所述步骤二中设计有限时间终端滑模控制器具体过程为:
利用NHDO对系统中的外界扰动和不确定性产生的复合干扰进行有效估计,在此基础上,基于有限时间滑模控制理论进行控制器设计。能够保证系统滑模面是有限时间稳定的,输出跟踪误差信号为渐近稳定的。
非齐次干扰观测器(NHDO)
考虑一阶的单输入单输出(SISO)非线性系统
其中,x表示系统状态,它的解是Filippov意义下的解,u∈R为连续的控制输入,d为充分光滑的不确定函数且m-1次可微,dm-1具有已知的Lipschitz常数L。设计如下NHDO;
式(11)中hi为如下的函数形式
其中,λi>0,μi>0,i=0,1,...,m。
假设系统(10)中的x和u(t)可测量且不存在量测噪声,所对应的参数λi,μi在逆序上充分大,则系统状态经历有限时间的暂态过程后,一定满足下列方程
z0=x,z1=d,…,zi=vi-1=g(i-1),i=1,…,m (13)
证明:令
对式(14)求导可得
式(15)为Filippov意义下的微分包含,可见包含中未知扰动d和控制输入u(t)的信息没有“记忆”。其余证明过程同文献(Peng L,Xuefeng P,Jianjun M,et al.Non-homogeneous disturbance observer-based second order sliding mode control for a tailless aircraft[C]//Chinese Automation Congress(CAC),2013.IEEE,2013:120-125),证毕。
文献(Peng L,Xuefeng P,Jianjun M,et al.Non-homogeneous disturbance observer-based second order sliding mode control for a tailless aircraft[C]//Chinese Automation Congress(CAC),2013.IEEE,2013:120-125)中,对于m≤5时给出参数λi和μi的一组有效数值为:λ0=8,λ1=5,λ2=3,λ3=2,λ4=1.5,λ5=1.1,μ0=12,μ1=11,μ2=10,μ3=8,μ4=6,μ5=3。
令则式(8)第二方程重写为
采用NHDO(17)来估计式(16)中系统干扰di的值。
由命题1可知,NHDO输出经历有限时间后收敛于di。
式(17)中观测器收敛速率取决于L值的大小,L的值越大收敛速率越大,但会引起系统出现瞬态峰值,因此需要折中选取L的值。
基于NHDO的快速非奇异终端滑模控制器设计
为了进一步提高系统收敛速率和增强系统抗扰动性能,本文给出的快速非奇异终端滑模面与文献(Zhu Z,Xia Y,Fu M.Attitude stabilization of rigid spacecraft with finite‐time convergence[J].International Journal of Robust and Nonlinear Control,2011,21(6):686-702),(Yang L,Yang J.Nonsingular fast terminal sliding‐mode control for nonlinear dynamical systems[J].International Journal of Robust and Nonlinear Control,2011,21(16):1865-1879),(Xu S S D,Chen C C,Wu Z L.Study of nonsingular fast terminal sliding-mode fault-tolerant control[J].IEEE Transactions on Industrial Electronics,2015,62(6):3906-3913)相比具有更快收敛速率。利用NHDO估计系统干扰值的大小,来提高了系统鲁棒性,并基于有限时间滑模理论,设计一种新颖的非奇异快速终端滑模控制器。具体过程如下。
选取非奇异终端滑模面:
r1=(2-γ)ηγ-1 (20)
r2=(γ-1)ηγ-2 (21)
其中,i=V,h,1<p/q<2,p和q为正奇数,γ>p/q,β>0,α>0,α0>0;
由于提出的新型快速终端滑模面(18)与文献(Yu X,Man Z.Model reference adaptive control systems with terminal sliding modes[J].International Journal of Control,1996,64(6):1165-1176)相比能够避免奇异问题,当时,并利用泰勒公式展开可得
因此,快速非奇异终端滑模面(18)与文献(Yang L,Yang J.Nonsingular fast terminal sliding‐mode control for nonlinear dynamical systems[J].International Journal of Robust and Nonlinear Control,2011,21(16):1865-1879),(Xu S S D,Chen C C,Wu Z L.Study of nonsingular fast terminal sliding-mode fault-tolerant control[J].IEEE Transactions on Industrial Electronics,2015,62(6):3906-3913)相比具有更快的收敛速率。
对滑模面(18)求导并结合式(8)整理得
其中,
设计终端滑模控制器如下:
其中,k1>0,k2>0、ε>2为非齐次干扰观测器的输出。
其它步骤及参数与具体实施方式一或二相同。
具体实施方式四:本实施方式与具体实施方式一至三之一不同的是:所述步骤三中对步骤二设计的有限时间终端滑模控制器进行系统稳定性证明的具体过程为:
对于系统(8),在满足假设1条件下,选择快速非奇异终端滑模面(18),在NHDO(17)和控制器(24)-(26)和作用下可得到如下结论。
(1)系统滑模面si是有限时间收敛的;
(2)变量和在有限时间内收敛到零。
证明:对于定理1的证明分为两步,(i)证明闭环系统状态在NHDO(17)估计系统干扰过程中是有界的。(ii)证明辅助误差变量和在有限时间内收敛到零。
(i)下面证明闭环系统状态在NHDO收敛过程中是有界的
将控制器(24)代入式(22)可得
当时,根据式(23)和式(25)整理得
当时,根据式(23)和式(25)整理得
由式(28)和式(29)整理得
定义辅助变量和如下:
对式(31)求导整理得
选取Lyapunov函数
对(33)沿系统轨线求导得
当时
当时
根据式(35)和式(36),式(34)可整理的
对于参数取值为1<p/q<2和ε>2,则式(34)中设计参数满足
根据则不等式成立,因此,式(34)可表示为
根据
根据式(40),则式(39)整理得
其中,
由命题1可知,其中Δ为正常数,则式(41)可改写为
其中,
根据式(42),Δ在有限时间内不会趋于无穷大,因此,整个闭环系统(8)中状态在非齐次干扰观测器的收敛阶段内是有界的;
证明系统滑模面si在有限时间内收敛到零。
非齐次干扰观测器经过时间tr满足因此,式(27)可改写为
定义辅助变量
对式(44)求导可得
其中,k1>0,k2>0,β>0,矩阵A为赫尔维茨的;
选择李雅普诺夫函数
V2=ηTPη (46)
其中,P为常值矩阵,满足黎卡提方程
ATP+PA=-Q (47)
其中,Q=QT>0
对式(46)求导
根据
由式(49)并联合则式(48)整理得
其中,
当根据式(45)中η在限时间内收敛到零,且收敛时间ts为
其中,V2(tr)在tr时刻的值,由式(44)得到滑模面si在有限时间内收敛到零;
当时,将控制器(24)代入式(8)可得
当t>tr时,对于si>0,对于si<0,因此不是吸引子;则系统滑模面si在有限时间内收敛到零;
系统滑模面si在有限时间内收敛到零,对误差辅助变量和稳定性分析如下:
当时,则式(18)变为
在有限时间内收敛到
当时,由式(18)可得:
和在区域内有限时间收敛到零;
利用泰勒公式展开可知,
则式(54)可整理为与文献(Yang L,Yang J.Nonsingular fast terminal sliding‐mode control for nonlinear dynamical systems[J].International Journal of Robust and Nonlinear Control,2011,21(16):1865-1879)滑模面形式类似,因此可参考其证明方法,可得和在tf内收敛到零;
系统(8)在设计的控制器(24)-(26)作用下,误差辅助变量σ1(x)和σ2(x)在有限时间内的收敛到零,则σV(x)、σh(x)为渐近收敛到零;系统(8)为公式(8)。
变量σ1(x)、σ2(x)在有限时间内收敛到零,则式(5)可写为
选取李雅普诺夫函数
对式(56)求导
由式(57)可知,和则σV(x)、σh(x)为渐近收敛到零。
其它步骤及参数与具体实施方式一至三之一相同。
实施例一:
为验证有限时间终端滑模控制器(24)-(26)的有效性。参考文献(Sun H,Li S,Sun C.Finite time integral sliding mode control of hypersonic vehicles[J].Nonlinear Dynamics,2013,73(1-2):229-244)高超声速飞行器参数和飞行环境参数见表1,空气动力学系数取值见表2。
表1飞行器参数和飞行环境参数
表2空气动力学系数取值
根据上述高超声速飞行器模型的基本参数可求出高超声速飞行器的一组平衡工作点。初始值x(0)=[4590.3 33528 0.0334 0.0334 0 0.1802 0]T。在仿真过程中,外界干扰取为d1(t)=0.0024sin(0.2t),d2(t)=0.012sin(0.2t),模型参数不确定性考虑如下:
m=m0(1+Δm),Iyy=I0(1+ΔIyy),
S=S0(1+ΔS),c=c0(1+Δc),
ce=ce0(1+Δce0),ρ=ρ0(1+Δρ), (58)
|Δm|≤0.05,|ΔIyy|≤0.05,|ΔS|≤0.05,
|Δc|≤0.05,|Δρ|≤0.05,|Δce|≤0.05.
其中,m0,I0,S0,c0,ce0,ρ0为对应的标称值,模型参数不确定性取为Δm=-0.05,ΔIyy=-0.05,Δc=0.05,Δce=0.05,Δρ=0.05,ΔS=0.05。
快速终端滑模的有限时间控制器仿真分析
为了验证所设计高超声速飞行器控制策略(24)-(26)的有效性,针对高超声速飞行器期望速度指令期望速度指令为Vd=4690.3m/s,即ΔV=100m/s,期望高度指令为hd=34528m,即Δh=1000m。观测器参数取为:λ0=1.1,λ1=1.5,λ2=2,μ0=3,μ1=6,μ2=8。控制参数选取如下:ε=2.1γ=1.8、η=0.01、α0=0.006、α1=0.05、α2=25、k1=0.001、k2=35、p/q=1.2。其仿真结果如图1-图9所示。
图1和图2为速度V跟踪曲线;图3和图4为高度h跟踪曲线,从图1-图4的仿真结果可得高超声速飞行器在有限时间终端滑模控制器(24)-(26)作用下能够实现对参考指令的快速稳定跟踪,且跟踪性能较好,满足跟踪性能要求。图5为高超声速飞行器控制输入曲线,从仿真曲线可看出系统快速收敛,且控制输入曲线光滑抖振很小。图6为高超声速飞行器其它状态量的变化曲线,从仿真曲线可看出,攻角α、俯仰角θ和俯仰角速率q在较短的时间内趋于其稳态值。图7给出了控制器中自适应参数的变化曲线,可以看出,自适应参数快速趋近于稳态值。图8和图9给出了有限时间NHDO对扰动估计曲线,从扰动估计曲线可知,NHDO有较快的收敛速度,可以有效消除跟踪静差,提高系统精度。
本发明基于有限时间滑模控制理论和NHDO对含有模型参数不确定性以及外界干扰情形下的高超声速飞行器跟踪问题进行研究分析。主要结论如下:
(1)基于反馈线性化模型,通过引入误差辅助变量,给出了带有系统干扰的多变量二阶系统模型,为方便其控制器设计提供了模型基础。
(2)针对带有系统干扰的高超声速飞行器多变量二阶系统模型,设计了带有NHDO的有限时间终端滑模控制器,通过引入了NHDO对复合干扰进行估计,有效降低了控制器增益,避免了通过增大系统增益提高控制系统抗扰动性能。
(3)利用李雅普诺夫理论对所设计的控制器给出了严格的理论证明,表明系统状态在NHDO对系统干扰估计的收敛阶段是有界的,并同时能够使得系统滑模面为有限时间稳定的,速度误差和高度误差为渐近稳定的。并对高超声速飞行器纵向非线性模型进行了数字模拟,进一步验证了表明了所设计控制器的有效性。
- 还没有人留言评论。精彩留言会获得点赞!