一种基于膜算法的永磁直流电动机转速在线控制方法与流程

本发明涉及永磁直流电动机转速控制技术领域，尤其涉及一种基于膜算法的永磁直流电动机转速在线控制方法。

背景技术：

目前，高性能的永磁直流电机在机器人、轧机、机床等工业中广泛应用。而对于这些高性能的永磁直流电机的使用，其核心问题在于对电机进行精确转速(位移)控制。由于高性能的永磁直流电机要求电机能够快速响应，转速能够从负载影响中快速复原，并且对参数变量不敏感，因此电机速度的精确控制是当前研究热点问题。

传统的永磁直流电机速度控制采用比例积分(PI)或者比例积分微分(PID)控制，这些控制算法能够使得一些线性系统在很小范围的系统参数内稳定。然而，这些控制系统对数学模型的精度有很高的要求，而精确的系统模型通常很难获得。同时，由于电机负载的不确定性并具有非线性机械特性，很可能造成驱动系统不稳定。

技术实现要素：

本发明的目的是提供一种基于膜算法的永磁直流电动机转速在线控制方法，能够在参数的灵敏性低，涉及参数较少的情况下实现高精度的转速控制。

本发明采用的技术方案为：

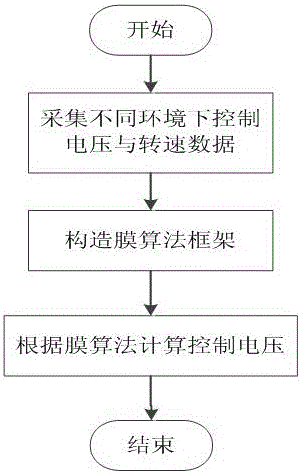
一种基于膜算法的永磁直流电动机转速在线控制方法，包括以下步骤：

步骤1：据永磁直流电机驱动系统动态模型推导所需建立模型的输入输出变量；

步骤2：根据不同工况收集转速与控制电压的数据，利用收集到的转速与对应控制电压数据分别构造高斯过程模型和二阶多项式模型；

步骤3：根据所构造的多项式响应模型和高斯过程预测模型构造三层膜的膜算法框架；

步骤4：首先，在步骤3获得膜算法框架中输入下一周期期望转速，得到预测控制电压v_c*；然后，将输出层预测控制电压v_c*输出，经D/A转换器转换后作用到永磁直流电机，当完成当前时刻转速控制后，更新膜算法内模型，继续执行下一时刻转速控制。

步骤3中所构造的膜算法，包含三层膜，最外层为多项式响应模型层，中层为高斯过程模型层，内层为输出层；其中，输出层将最外层的预测控制电压和中层的预测电压加权并输出到D/A转换器，其加权函数为v_c*＝v_cPR(1-α)+v_cKriα，其中α的取值范围为[0.9,0.95]，v_cPR为外层预测值，v_cKri为中层预测值，v_c*为最终输出控制电压。

步骤3中膜算法的外层多项式模型层为三输入二阶多项式模型，可以根据预测粗略预测控制电压；中层高斯过程模型层为三输入一输出高斯过程预测模型，可以更高精度的预测控制电压；内层输出层能够接收外层和中层的预测输出，然后权衡两个输出得到更为准确的输出。

步骤3构造多项式模型为：

其中输入ω(n-1)＝x₁,ω(n+1)＝x₂,ω(n+1)＝x₃，输入为控制电压v；对于该多项式模型，通过权利要求1步骤2中采集的输入输出数据，根据最小二乘法可以计算出模型参数b₀,b₁,…,b₉。

步骤2构造的高斯过程控制器模型如下：

其中θ是核函数弯曲程度，本发明中取5，r^T_100×1(x)＝[R(θ,x,x₁)…R(θ,x,x₁₀₀)]^T，且以及设计矩阵x是权利要求1步骤2中采集的转速,F是权利要求1步骤2中采集的控制电压。

膜算法作为一种具有高度并行性的生物启发算法，能够具备良好的全局和局部寻优能力，本发明通过膜算法的并行性，能够快速预测，同时通过不同膜之间的通信，增强了不同模型的预测效果，最终能够实现高精度的转速控制，同时该方法对参数的灵敏性要求很低，涉及参数很少。

附图说明

图1为本发明的流程图；

图2为本发明所述膜算法的框架图；

图3为本发明控制示意图。

具体实施方式

以下结合附图对本发明的原理和特征进行描述，所举实例只用于解释本发明，并用非用于限定本发明。

如图1、2和图3所示，一种基于膜算法的永磁直流电动机速度控制方法，包括以下步骤：

步骤1：根据永磁直流电机驱动系统的控制电压与各元件的电压平衡和电机负载转矩与开发转矩、摩擦转矩的平衡推导所需建立电压电流以及转矩随着时间和负载改变的数学模型(如(1)所示)。

其中v_a(t)，e_b(t)和i_a(t)分别是时变电机端电压，反电动势和电枢电流；ω_r(t)是电机转速，R_a和L_a分别是点数电阻和电感；K_T和K_E是电机反电动势和转矩常数，T_e(t),T_l(t)和T_F分别是开发转矩，负载转矩和摩擦转矩；J和B则是惯性常数和粘性常数。

并且负载转矩和转速间的关系可以描述为：

T_l(t)＝vω_r²(t)[sign{ω_r(t)}]，其中v是构造非线性机械负载的常数。

因此，通过差分方程可以得到电机转速与控制电压关系离散模型为

ω_r(n+1)＝K₁ω_r(n)+K₂ω_r(n-1)+K₃[sign{ω_r(n}]ω_r²(n)

+K₄[sign{ω_r(n}]ω_r²(n-1)+K₅v_a(n)+K₆

其中K₁,K₂,K₃,K₄,K₅,K₆是关于电机参数的常数，同样该模型可以形式化为3输入1输出的函数v_c(n)＝f[ω_r(n+1),ω_r(n),ω_r(n-1)]，其中v_c(n)是控制电压并且与v_a(n)成比例。

步骤2：采集M组输入为转速与输出为控制电压的数据；

步骤3：根据步骤1推导的电机离散模型，设计输入为ω_r(n+1),ω_r(n)和ω_r(n-1)，输出为v_c(n)的电机转速与控制电压关系的高斯过程模型y(x)＝F^T(x)β+Z(x)；其中F(x)＝a₂x²+a₁x+a₀(通过步骤2中所采集的转速为输入，以控制电压为输出，采用最小二乘法可以求得函数参数a₂、a₁、a₀),Z(x)是均值为0方差为的涨落函数，其协方差矩阵为其中是高斯过程模型的核函数，θ_k是核函数的弯曲程度(通常取5)，x_i,x_j是输入向量x的第i个和第j个维度的变量，且x＝[ω_r(n-1)ω_r(n)ω_r(n+1)]^T，z_i,z_j是涨落函数Z(x)对应输入x的第i个和第j个维度的输出，T表示矩阵转置操作；

步骤4：将步骤2采集的M组数据输入步骤3获得的高斯过程模型，假设步骤2采集的输入x是m维的数据时(根据步骤1推导得到，m＝3)，x的各个维度间的关联矩阵为函数F(x)通过F(x)＝a₂x²+a₁x+a₀计算的结果为控制电压为vci为第i组控制电压。

然后，构造基于上述数据更新得到的的高斯过程预测模型为：

其中r^T_m×1(x)＝[R(θ,x,x₁)…R(θ,x,x_m)]^T，为预测控制电压，为模型相关参数。

步骤5：根据步骤1推导的电机离散模型，设计输入为ω_r(n+1),ω_r(n)和ω_r(n-1)，输出为v_c(n)的二阶多项式模型。令ω(n-1)＝x₁,ω(n+1)＝x₂,ω(n+1)＝x₃，则构造的控制电压与转速模型为通过步骤2中获取的M组输入输出数据，通过最小二乘法辨识未知参数b₀,b₁,…,b₉。

步骤6：根据步骤5所构造的多项式响应模型和步骤4所构造的高斯过程预测模型，构造三层膜的膜算法框架，最外层为多项式响应模型层，中层为高斯过程模型层，内层为输出层。其中，输出层为外层和中策预测控制电压的权衡，其权衡函数为v_c*＝v_cPR(1-α)+v_cKriα，其中α的取值范围为[0.9,0.95]，v_cPR为外层预测值，v_cKri为中层预测值。

步骤7：输出输出层控制电压作用到永磁直流电机，得到对应转速，更新膜算法内模型。

以下以具体实例进行举例说明，实际操作时，M取101时，操作步骤为：

步骤1：采集101组转速与控制电压数据，构造100组输入为x＝[ω_r(n-1) ω_r(n) ω_r(n+1)]^T，输出为Y＝v_c(n)的数据集。

步骤2：根据步骤1采集的数据，采用最小二乘法拟合输入为ω_r(n+1),ω_r(n)和ω_r(n-1)，输出为v_c(n)的二阶模型F(x)＝a₂x²+a₁x+a₀，计算出未知参数a₀,a₁,a₂。同时根据步骤1采集的数据和电机控制电压与转速的关系，构造输入为ω_r(n+1),ω_r(n)和ω_r(n-1)，输出为v_c(n)电机转速与控制电压关系的高斯过程预测模型：

其中θ是核函数弯曲程度，本发明中取5，r^T_100×1(x)＝[R(θ,x,x₁)…R(θ,x,x₁₀₀)]^T，且以及设计矩阵

步骤3：根据步骤1采集的数据，采用最小二乘法拟合输出为控制电压输入为转速的二阶多项式响应模型其中ω(n-1)＝x₁,ω(n)＝x₂,ω(n+1)＝x₃，计算出模型参数b₀,b₁,…,b₉。

步骤4：首先在步骤2得到的高斯过程预测模型中输入下一周期目标转速ω(n+1)^*，得到预测控制电压v_cPR；

然后，在步骤3得到的二阶多项式响应模型中输入下一周期目标转速ω(n+1)^*，得到预测控制电压v_cKri；

最后，将得到的两个预测控制电压输出到输出层，利用权衡函数v_c*＝v_cPR(1-α)+v_cKriα权衡预测得到的两个不同的控制电压，将获得权衡后的控制电压输出，其中α的取值范围为[0.9,0.95]。

步骤5：将由步骤4得到的权衡后的控制电压v_c*输出到控制电路，经D/A转换器转换后作用到永磁直流电机，当完成当前时刻转速控制后，重复步骤2、4、5。

如图2所示，基于膜算法的永磁直流电机转速控制包含了两个模型。第一个模型是二阶多项式响应模型，具有较好的全局搜索能力，但是精度较差；第二个模型是高斯过程模型，具有较好的局部搜索能力，但是有可能陷入局部最优。通过膜算法结合了两个模型的优点，能够在很大程度上提高模型的鲁棒性和全局搜索能力和搜索精度。

构造的电机转速与控制电压装置原理如图3所示，包含了电机离散控制的基本装置。本发明所提出的膜算法能够并行的构造代价低的多项式模型和代价高的Kriging模型，通过不同层次膜之间的通信，获得不同模型中的更优解，具有更高准确性的预测能力和更强的鲁棒性，能够实现永磁直流电动机转速更高精度的控制。

以上所述仅为本发明的较佳实现例，并不用以限制本发明，凡在本发明的精神和原则内，所做的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。