一种基于神经网络的算法解决作业车间调度问题的利记博彩app
本发明涉及作业车间调度技术领域。
背景技术:
作业车间调度问题(Job-Shop Scheduling Problem,JSP)是制造执行系统研究的核心和重点之一,它的研究不仅具有重大的现实意义,而且具有深远的理论意义。JSP就是根据产品制造需求合理分配资源,进而达到合理利用产品制造资源、提高企业经济效益的目的。JSP是产品制造行业中共存的问题,它与计算机集成制造系统(Computer Integrated Manufacturing Systems,CIMS)的工厂管理、产品制造层次紧密相关,是CIMS领域中研究的重要课题。JSP是一个典型的NP-hard问题,它的研究必然会对NP问题的研究起到有意义的影响。
人工神经网络是模仿生物脑结构和功能的一种信息处理系统,它是一种大规模的并行结构,信息的分布式存储和并行处理,具有良好的自适应、自组织和容错性,具有较强的学习、记忆、联想和识别功能等。它的主要思想是用人工神经元相互连接组成一个计算机网络,并行高效地求解问题。神经网络解决车间调度问题的主要思路是:通过一个Lyaplmov能量函数构造网络的极值,当网络迭代收敛时,能量函数达到极小,使与能量函数对应的目标函数得到优化。
但神经网络的效率受训练影响很大,并且在问题规模较大时,存在计算速度慢与结构参数难以确定的弱点。
技术实现要素:
针对现技术存在的上述不足,本发明要解决的技术问题是提供一种新的基于神经网络算法解决作业车间调度问题。
本发明的目的是克服现有技术中存在的:在问题规模较大时,存在计算速度慢弱点。
本发明为实现上述目的所采用的技术方案是:一种基于神经网络的算法解决作业车间调度问题,该算法的主要步骤如下:
步骤1:设置时间t,常量A,B,C的初始值,A,B,C>0,是常数;
步骤2:初始化系数矩阵W
步骤3:构造阈值向量
步骤4:构造状态函数
步骤5:计算关系函数
步骤6:构造能量函数
步骤7:计算神经输入偏置电流(外加激励)Ixi
步骤8:调整系数矩阵
步骤9:确定运行方程
步骤10:根据四阶龙格—库塔(runge_kutta)公式计算vxi(t+1)
步骤11:判断是否达到平衡条件
本发明的有益效果是:
1、通过平均阈值构造阈值向量,在一定程度上减少了算法的计算量。
2、通过将能量函数与标准能量函数做比较,对权值系数作修正,使算法的解更加精确,同时加快了算法的收敛性,减少了不必要的搜索时间。
3、通过加入仿双极S型函数对神经元状态进行逼近更新,算法更加精确。
附图说明
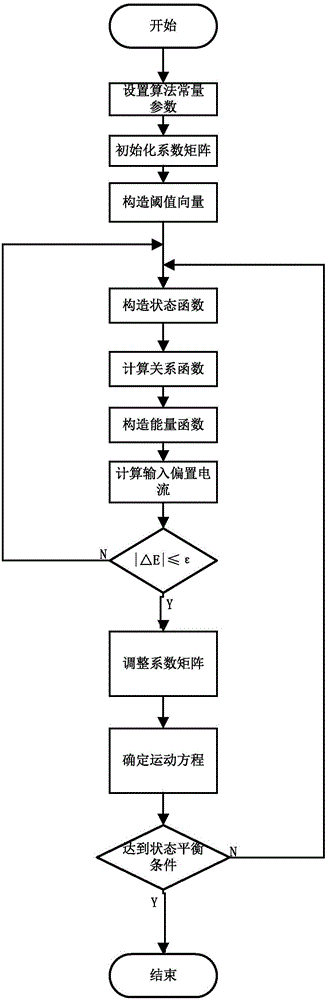
图1表示本发明的基本流程图
图2表示神经网络算法的分层示例图
具体实施方式
以下结合附图,对本发明进行详细说明。
神经网络算法,结合图2,可看出其分为输入层、隐含层、输出层三层,在作业车间调度问题中,把工件的状态抽象作为神经网络中的输入单元。
根据以上原理,结合图1,本算法的详细实施步骤如下。
步骤1:设置时间t,常量A,B,C的初始值,A,B,C>0,是常数;
步骤2:初始化系数矩阵W:对于一个由n个神经元组成的离散Hopfield网络,则有n*n权系数矩阵W:
W={wij},i,j=1,2,...,n
步骤3:构造阈值向量:有n维阈值向量θ:
θ=[f(θ1),f(θ2),...,f(θn)]T
其中,c是一个平均阈值,
一般而言,W和θ可以确定一个唯一的离散Hopfield网络net=W×θ;
步骤4:构造状态函数:用Yj(t)表示第j个神经元,即节点j在时刻t的状态,则节点的下一个时刻(t+1)的状态可以求出如下:
步骤5:计算关系函数:计算神经元之间的关系函数Wxi,yi:
Wxiyj=-Aδxy(1-δij)-B-Cδi1δj1
其中
步骤6:构造能量函数:E=E1+E2+E3
行约束条件:
其中,Vxi表示第i个神经元的状态V=Y;A>0,为常数,E1为行约束,当且仅当每个矩阵航中均不含有多于一个“1”元素,其余元素均为“0”时,E1保证当矩阵v的每一行不多于一个“1”时,E1到达最小,此时E1min=0;
同理,构成列约束条件
其中,B>0,为常数,E2保证当矩阵v的每一行不多于一个“1”时,E2到达最小E2min=0;
全局约束条件:
其中,C>0,为常数,E3保证当矩阵V中的恰好为mn个1,即整个矩阵中一共有mn个1,E3达到最小E3min=0;
步骤7:计算神经输入偏置电流(外加激励)Ixi;
步骤8:调整系数矩阵:
首先,求步骤4中的能量函数与标准能量函数之间的能量差:
标准能量函数为:
能量差:
ΔE=E-Em
如果|ΔE|≤ε,返回步骤4,否则转步骤9,根据这个能量差对权值系数Wxiyj作调整,调整方式如下:
Wxiyj=-Aδxy(1-ΔE)-B-Cδi1δj1
步骤9:确定运行方程:计算Vxi(t),每个神经元输出与输入之间满足Sigmoid函数特性,设置u0初始值:
其中,
Sigmoid函数使g(vxi)在0到1之间取值,为了避免工件被部分的调用(部分使用资源),开始给v0一个较大的值,从而能用一个较低的增益来迭代网络,经过一定次数的迭代后,v0的值显著减小,将增益提高到一个较大的值,对于较大的增益,Sigmoid函数和硬限幅函数相似,神经元的输出值接近于1,这样可以避免干扰部分调度的问题,同时也可以避免采用限幅函数而引起的网络不稳定;
式中的τ=Rxi=Cxi为时间常数,为了简便,设τ=Rxi=Cxi=1;
为了满足约束条件,可以对某些神经元进行强抑制,使得这些神经元不被触 发,根据JSP的每个工序不允许自依赖,所以矩阵中(i,i+1)(i=0,1,…,mn)位置的神经元应为电流;对于有优先次序关系的和不允许在0时刻启动的工序,在其矩阵的响应位置设置0电流,使这些神经元在稳态输出时为0,计算能量式为最小;
步骤10:根据四阶龙格—库塔(runge_kutta)公式计算vxi(t+1):
K1=f(xi,vxi(t))
K4=f(xi+h,vxi(t)+hK3`)
其中,f(xi,vxi(t))为仿双极S型函数:
步骤12:判断是否达到平衡条件:是,则结束此程序;否,则返回步骤4;
(1)状态平衡条件:利用神经元动态计算方程,计算Δvxi(t),
若网络从某一时刻以后,状态不再发生变化,则称网络处于稳定状态,此时满足
Δvxi(t)∈(0,c)
v(t+Δt)=v(t),Δt>0
(2)能量平衡条件:能量函数在网络运行中不断降低,最后达到稳定ΔEi≤0
。
- 还没有人留言评论。精彩留言会获得点赞!