基于CS‑Jerk模型的参数自适应机动目标跟踪算法的利记博彩app
本发明属于雷达目标跟踪领域,具体涉及一种基于cs-jerk模型的参数自适应机动目标跟踪算法。
背景技术:
雷达信号处理和雷达数据处理是现代雷达系统的核心技术,目标跟踪是雷达数据处理过程的关键技术之一。在获取目标位置及各项运动参数(如速度、方位、俯仰角等)后,可以通过目标跟踪算法对这些量测数据进行滤波、平滑、预测等处理,来减少甚至消除量测形成的随机误差,精确估计目标的运动状态参数,实现目标航迹的预测。
目标跟踪技术主要包括两个方面,一是构建目标运动模型,二是滤波算法设计,且滤波算法建立在目标运动模型基础之上。机动目标运动模型的建立需要综合考虑多种因素,既要尽可能地使模型与实际运动状态一致,模型的运算量又不能太大。最早提出的也是最为经典实用的是匀速(constantvelocity,cv)模型、匀加速(constantacceleration,ca)模型以及协调转弯(coordinatedturn,ct)模型,适用于机动性较弱的目标。对于机动性较强的目标,r.a.singer在1970年提出了singer模型,它是一种零均值、一阶时间相关的机动目标运动模型。singer模型将目标的机动加速度看做时间相关的有色噪声,目标的加速度在最大加速度和最小加速度之间服从均匀分布。1984年,有学者提出了“当前”统计(currentstatistical,cs)模型。该模型用修正瑞利分布来描述目标加速度的统计特性,是一种非零均值的时间相关模型,是目前公认的较为准确的目标运动模型。对于高机动目标,kishore和mahapatraibg两人在1997年提出了jerk模型,qiaoxiangdong在2002年提出了一种当前统计机动(cs-jerk)模型,戴邵武在2016年提出了一种改进的cs-jerk模型,该模型与目标真实机动情况更加符合。
针对高机动目标跟踪方法,发明专利cn201210138397.1公开了一种高机动目标跟踪方法,主要通过建立改进jerk模型,改善现有技术中目标高机动带来的模型不匹配和跟踪精度低的问题;发明专利cn201310404989.8公开了一种基于残差反馈的多模型高速高机动目标跟踪方法,主要通过lms算法,利用残差反馈降低多模型滤波的计算量。上述两种方法均需要人为设定过程协方差矩阵参数,无法实现对高机动目标的自适应跟踪。
技术实现要素:
本发明的目的在于提供一种基于cs-jerk模型的参数自适应机动目标跟踪算法,解决传统高机动目标cs-jerk模型需要人为设定过程协方差矩阵参数的问题。
实现本发明目的的技术方案为:一种基于cs-jerk模型的参数自适应机动目标跟踪算法,包括如下步骤:
步骤1,建立当前-统计jerk模型;
步骤2,建立参数自适应的cs-jerk模型,具体为:
利用截断概率分布描述目标加速度变化率当前概率密度,得出目标加速度变化率方差与jerk均值的关系,实现对目标加速度变化率方差的自适应调整,同时利用残差向量判断目标机动情况的变化,通过非线性的机动频率函数对机动频率的自适应调整,实现过程协方差矩阵的自适应调整;
步骤3,建立基于acs-jerk模型的卡尔曼滤波算法。
与现有技术相比,本发明的显著优点为:
(1)本发明基于cs-jerk模型的参数自适应(acs-jerk)目标跟踪算法在传统的卡尔曼滤波反馈回路中加入了距离函数计算、机动门限检测、加速度变化率方差更新以及机动频率修正这四个环节,实现了滤波跟踪算法的自适应调整,提高了目标跟踪精度,减少了模型误差;(2)本发明增强了对高机动目标运动过程变化的自适应能力,在工程实际中具有较好的应用价值。
附图说明
图1是本发明方法的实现流程图。
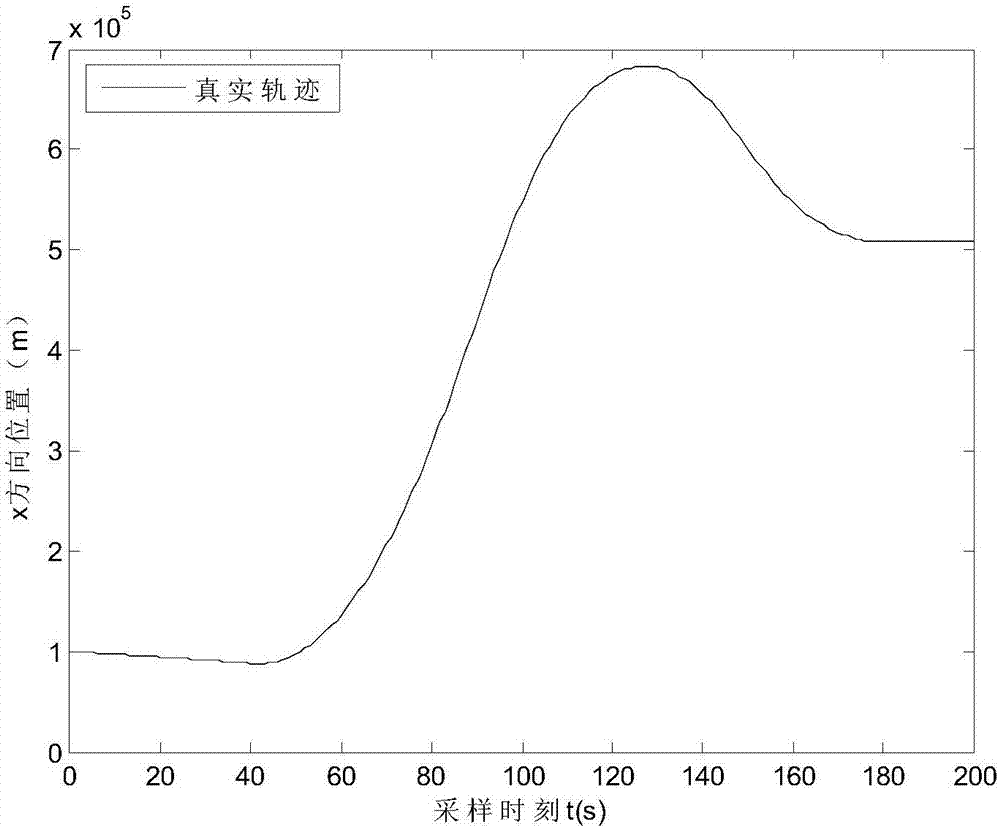
图2是目标的真实运动轨迹图。
图3是本发明方法与cs-jerk在目标跟踪轨迹上的比较图。
图4是本发明方法与cs-jerk在x方向位置均方根误差比较图。
图5是本发明方法与cs-jerk在x方向速度均方根误差比较图。
图6是本发明方法与cs-jerk在x方向加速度均方根误差比较图。
具体实施方式
结合图1,一种基于cs-jerk模型的参数自适应机动目标跟踪算法,包括如下步骤:
步骤1,建立当前-统计jerk模型;
步骤2,建立参数自适应的cs-jerk模型,具体为:
利用截断概率分布描述目标加速度变化率当前概率密度,得出目标加速度变化率方差与jerk均值的关系,实现对目标加速度变化率方差的自适应调整,同时利用残差向量判断目标机动情况的变化,通过非线性的机动频率函数对机动频率的自适应调整,实现过程协方差矩阵的自适应调整;
步骤3,建立基于acs-jerk模型的卡尔曼滤波算法。
进一步的,步骤1具体为:
cs-jerk运动模型由四个状态分量组成,位置、速度、加速度以及加速度变化率;
t时刻的状态向量为:
假设目标的加速度变化率是非零均值的时间相关随机过程,即
其中
其中
应用维纳—柯尔莫哥洛夫白化算法,将有色噪声j(t)表示为白噪声ω(t)驱动的结果,可得
其中白噪声ω(t)的方差为
经过离散化处理后,cs-jerk模型的离散状态方程为
x(k)为状态变量,u为输入控制矩阵,w(k)为离散化的白噪声,f为离散化后的状态转移矩阵,
其中,t为采样周期,
白噪声w(k)的过程噪声协方差矩阵是:
cs-jerk模型将当前时刻目标加速度变化率的一步预测
进一步的,步骤2具体为:
步骤2-1,利用截断概率分布描述目标加速度变化率当前概率密度,得出目标加速度变化率方差与jerk均值的关系,实现对目标加速度变化率方差的自适应调整;
假设机动加速度变化率的当前概率密度用截断正态分布来描述,随机变量的概率分布指标是由正态分布的方差σj2描述,根据切比雪夫不等式:当随机变量服从正态分布时,随机变量与其数学期望的偏差落在3倍其均方差的范围之外的概率上限为0.003;假设:
则目标的机动加速度变化率的方差σj2与均值
jmax为目标加速度变化率的最大值,均值
步骤2-2,利用残差向量判断目标机动情况的变化,通过一种非线性的机动频率函数对机动频率的自适应调整,实现过程协方差矩阵的自适应调整;
在卡尔曼滤波算法中,残差向量为:
z(k)=h(k)x(k)+v(k)为量测向量,v(k)是零均值高斯白噪声序列,协方差为r(k),h(k)=[1000]为量测矩阵,
残差向量协方差为:
s(k)=h(k)p(k/k-1)ht(k)+r(k)(15)
p(k/k-1)=f(k/k-1)p(k-1/k-1)ft(k/k-1)+q(k-1)为预测估计误差协方差,f(k/k-1)为k-1时刻的状态转移矩阵,q(k-1)为过程噪声协方差,r(k)为量测噪声协方差;
定义距离函数为:
d(k)=dt(k)s-1(k)d(k)(16)
根据残差向量的统计特性可知,d(k)服从χ2分布;如果目标发生机动,残差向量d(k)将不是零均值高斯白噪声,d(k)将会变大;假设机动检测门限为m,若距离函数d(k)>m,则判定目标的机动情况发生变化,应当适当增大机动频率α的值;若距离函数d(k)≤m,则判定目标的机动情况未发生变化,应当适当减小机动频率α的值;为了体现机动频率α与距离函数d(k)的对应关系,定义机动频率α为:
其中,α0表示机动频率的初始值,按经验取值,如果目标做逃避机动,则α0=1/60;如果目标做转弯机动,则α0=1/20,如果目标仅受到环境扰动,取α0=1;该非线性函数变化的范围大,自适应变化比普通线性方程快,从而能根据目标机动情况有效地对α进行自适应调整。
acs-jerk模型利用当前时刻目标机动加速度变化率的估计值
进一步的,步骤3具体为:
对acs-jerk模型进行经典的卡尔曼滤波,其主要方程如下:
其中,
下面结合附图和实施例对本发明进一步说明。
实施例
实施例条件:在平面直角坐标系中,目标在x方向的情况,目标初始位置10000m,目标的速度、加速度初值和加加速度初值分别设定为-300m/s,0m/s2和0m/s3,量测噪声在运动过程中量测噪声服从n(0,1002)的高斯分布,仿真时长为200s,采样周期为1s。目标运动情况如下:
1)从0s开始,经过40s,以-300m/s的速度做匀速直线运动;
2)从40s开始,经过40s,;以300m/s2的加速度做匀加速运动;
3)从80s开始,经过20s,以-60m/s3的加加速度做匀加加速度运动;
4)从100s开始,经过20s,以10m/s3的加加速度做匀加加速度运动;
5)从120s开始,经过20s,维持匀加速运动;
6)从140s开始,经过20s,以60m/s3的加加速度做匀加加速度运动;
7)从160s开始,经过20s,维持匀加速运动;
8)从180s开始,经过20s,维持匀速直线运动。
目标运动的真实轨迹如图2所示。
cs-jerk模型中目标机动频率α取为1,目标jerk方差(加加速度方差)σj2=8m/s2。在acs-jerk模型中机动频率的初始值α0同样取为1,目标最大jerk机动设定为400m/s3,将机动门限m取为200。
分别对acs-jerk模型和cs-jerk模型的目标跟踪算法进行200次的蒙特卡洛仿真,这两种算法的局部跟踪轨迹比较如图3所示,在x方向上的位置、速度、加速度均方根误差如图4、图5、图6所示。图中,acs-jerk指代本发明方法;cs-jerk指代基于“当前”统计(cs)jerk模型的目标跟踪算法。
由图3可以看出acs-jerk算法跟踪性能优于cs-jerk算法。从图4、图5、图6的均方根误差对比图可以看出,目标在前40s做匀速直线运动时,本发明提出的acs-jerk模型目标跟踪算法与cs-jerk模型目标跟踪算法滤波效果几乎一致;而当目标从第40s开始到80s做匀加速直线运动时,两种算法都有一个滤波跟踪误差收敛的过程,acs-jerk模型滤波效果略优于cs-jerk模型;80s到100s、140s到160s时,目标做加加速度比较大的机动运动,能够很明显地观察出acs-jerk滤波精度比cs-jerk模型的精度要高出很多。在目标由强机动转变为弱机动的过程中acs-jerk滤波性能优越性表现的更加明显,如在第100s,acs-jerk滤波算法的位置、速度、加速度误差均方根值更小,原因在于当目标的加加速度出现变化时,cs-jerk模型滤波算法不能实现自适应调整,但是本文提出的acs-jerk滤波算法从两方面提升了模型的自适应性能,提升了算法对目标机动变化的滤波灵敏度。从整体来看,acs-jerk模型目标跟踪算法相较于cs-jerk模型目标跟踪算法滤波效果改进明显。
本发明利用截断概率分布描述目标加速度变化率当前概率密度,实现对目标加速度变化率方差的自适应调整,同时利用残差向量判断目标机动情况的变化,通过一种非线性的机动频率函数实现对机动频率的自适应调整,最终实现了过程协方差矩阵q(k)的自适应调整,有效地提高了目标跟踪精度,进一步增强了对高机动目标运动过程变化的自适应能力,在工程实际中具有较好的应用价值。
- 还没有人留言评论。精彩留言会获得点赞!