一种汽车轮心实际行驶位移测量与提取方法与流程
本发明涉及汽车检测领域,特别的涉及一种汽车轮心实际行驶位移测量与提取方法。
背景技术:
在对车身和车架进行动应力计算、疲劳仿真分析及振动分析等工作中,需要提供振动位移数据。而在进行实车测试时,由于仪器设备和环境的限制,要测得试验车测点的振动位移响应曲线是比较困难的,有时甚至是无法直接测量的。
目前,整车道路试验中,测量车轮轮心位移主要是通过拉线式、电位计式或激光式位移感器来进行的,但这三种位移传感器在道路试验中均存在局限性。拉线式位移传感器的频率响应过低,高频时有较多误差;电位计式传感器精度较高,但安装困难;激光式传感器需要有反射面,且易被灰尘和光照亮度等环境因素影响。
技术实现要素:
针对上述现有技术的不足,本发明所要解决的技术问题是:如何提供一种便于测量,精度较高,受环境因素影响较小的汽车轮心实际行驶位移测量与提取方法。
为了解决上述技术问题,本发明采用了如下的技术方案:
一种汽车轮心实际行驶位移测量与提取方法,其特征在于,包括如下步骤:
a、将加速度传感器安装在待测量汽车车轮的轮心位置上,对轮心的加速度数据进行采样;
b、对采样到的加速度数据进行平滑处理,消除高频噪音;
c、将步骤b中平滑处理后的加速度数据的时域信号作傅里叶变换成频域信号,得到轮心的加速度信号在任一频率下的傅里叶分量表达式为:
a(τ)=Aejωτ
式中,a(τ)为轮心加速度信号在频率ω的傅里叶分量;A为对应a(τ)的系数;j为虚数;
d、对轮心加速度信号在任一频率下的傅里叶分量的一次积分得轮心速度信号分量为:
式中,V(t)为轮心加速度信号在频率ω的傅里叶分量;V为对应V(t)的系数,
对轮心加速度信号在任一频率下的傅里叶分量的两次积分得到轮心位移分量为:
式中,X(t)为轮心速度信号在频率ω的傅里叶分量;X为对应X(t)的系数,
e、对上述公式(1)和(2)进行傅里叶逆变换即可得出轮心实际行驶速度信号和轮心实际行驶位移信号。
作为优化,所述步骤b中对采样到的加速度数据进行平滑处理具体为基于最小二乘法原理采用如下公式:
对轮心的加速度数据进行离散数据的直线滑动平均;
式中,y为轮心加速度数据经平滑处理后的结果;x为轮心加速度采样数据;m为数据点数;2N+1为平均点数。
作为优化,在所述步骤c前,先运用Welch方法(平均周期图法)对轮心加速度数据的自功率谱密度函数进行求解,将轮心的加速度信号转移至频域来观察其相对幅值,将加速度相对幅值小于0.001g的高频信号确定为趋势项和噪声干扰,确定步骤c中积分变换的通带频率范围。
综上所述,本发明方法具有如下优点:采用加速度传感器采集轮心位置振动信号并对其进行积分变换得到轮心实际行驶位移,具有传感器的安装方便,检测的灵敏度较高,采样频率范围较宽,受环境因素影响较小。另外,运用Welch方法能够准确确定积分变换的通带频率范围,消除高频噪音,提高了积分变换的准确性,有利于提高测量精度。
附图说明
图1为安装在轮心处的位移传感器所采样的轮心位移数据示意图。
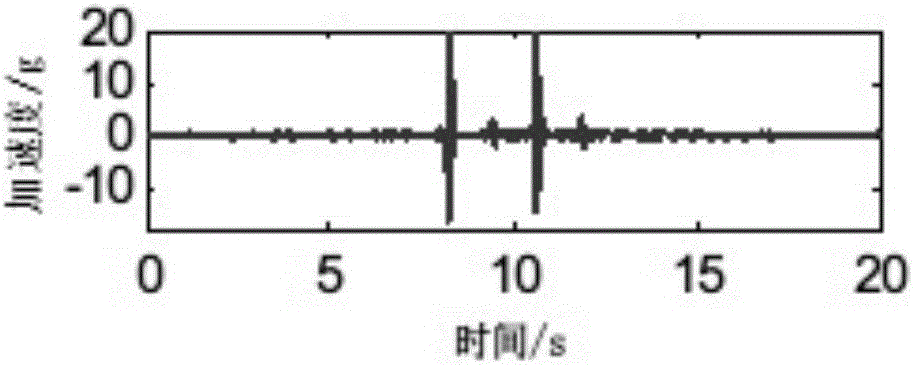
图2为安装在轮心处的加速度传感器所采样的轮心加速度数据示意图。
图3为原始采样到的加速度数据平滑处理前后结果对比示意图。
图4为图3的局部放大图。
图5为采用Welch方法确定积分变换的通带频率范围前积分结果与位移传感器实测数据对比示意图。
图6为运用Welch方法得到的加速度数据自功率谱幅频曲线。
图7为采用Welch方法确定积分变换的通带频率范围后积分结果与位移传感器实测数据对比示意图。
图8为图7的局部放大图。
具体实施方式
下面结合附图对本发明作进一步的详细说明。
一种汽车轮心实际行驶位移测量与提取方法,其特征在于,包括如下步骤:
a、将加速度传感器安装在待测量汽车车轮的轮心位置上,对轮心的加速度数据进行采样;
b、对采样到的加速度数据进行平滑处理具体为基于最小二乘法原理采用如下公式:
对轮心的加速度数据进行离散数据的直线滑动平均;
式中,y为轮心加速度数据经平滑处理后的结果;x为轮心加速度采样数据;m为数据点数;2N+1为平均点数。
运用Welch方法(平均周期图法)对轮心加速度数据的自功率谱密度函数进行求解,将轮心的加速度信号转移至频域来观察其相对幅值,将加速度相对幅值小于0.001g的高频信号确定为趋势项和噪声干扰,确定步骤c中积分变换的通带频率范围。
c、将步骤b中平滑处理后的加速度数据的时域信号作傅里叶变换成频域信号,得到轮心的加速度信号在任一频率下的傅里叶分量表达式为:
a(τ)=Aejωτ
式中,a(τ)为轮心加速度信号在频率ω的傅里叶分量;A为对应a(τ)的系数;j为虚数;
d、对轮心加速度信号在任一频率下的傅里叶分量的一次积分得轮心速度信号分量为:
式中,V(t)为轮心加速度信号在频率ω的傅里叶分量;V为对应V(t)的系数,
对轮心加速度信号在任一频率下的傅里叶分量的两次积分得到轮心位移分量为:
式中,X(t)为轮心速度信号在频率ω的傅里叶分量;X为对应X(t)的系数,
e、对上述公式(1)和(2)进行傅里叶逆变换即可得出轮心实际行驶速度信号和轮心实际行驶位移信号。
为进一步说明,结合如下实施例对本发明方法进行说明:
为了解车辆在极端工况下的受力状态,选取了汽车试验场试验中的路缘冲击工况进行试验并采集数据。路缘冲击试验是整车可靠性道路试验的一部分,将车辆以某一车速经过一段一定高度的突起路面,用于评估车轮冲击路缘石时对整车结构的影响。
选取某量产车型进行试验,提前在试验车后轮轮心位置布置了加速度传感器和位移传感器,其中,加速度传感器为KISTLER电容式MEMS三轴加速度计,位移传感器为YKD拉线式位移传感器。两个传感器均布置于车轮轮心位置,空间坐标系选取遵从笛卡尔坐标系,与整车坐标系一致,依据ISO4130-1978《道路车辆三维参考系统和基准符号定义》。
将试验车在汽车试验场以50km/h的速度经过路缘冲击路段,采集右后轮心的位移和加速度数据曲线,如图1和图2所示。数据采样频率为1024Hz,数据长度约为20s。采样数据在第8.2s左右的第一次冲击峰值是右后轮冲上路缘时产生的,第10.5s左右的第二次冲击峰值是右后轮冲下路缘时产生的,第9.5s和12s左右的小峰值是左后轮冲击路缘时波及到右后轮时对其造成的扰动。
从试验数据曲线中可以看出,位移曲线波动幅度较大,前5s为车辆加速阶段,后轮弹簧压缩,相对位移趋向负值;12s之后为车辆减速阶段,后轮弹簧拉伸,相对位移趋向正值。相对位移曲线的变化情况与实际试验情况一致,为之后的积分结果提供了良好的验证数据;加速度曲线稳定在零点附近,并没有出现明显的趋势项,信号状态优良,为之后的积分处理提供了良好的源数据。
采样数据的预处理
对采样数据进行预处理使其尽可能的接近真实值是最基本的数据加工方式。在振动测试中,环境温度、电磁干扰等都会造成放大器的零点漂移,使测试得到的数据中含有一定程度的直流分量和噪声信号。这些污染信号的存在会使数值积分的结果产生很大误差,甚至完全背离真实情况,需要在数据预处理中对其进行清除。
对采样到的加速度信号数据进行平滑处理
通过数据采集设备采样得到的振动信号往往叠加有随机干扰信号。随机干扰信号具有较宽的频带,有时还带有相当比例的高频成分,使得振动曲线出现多毛刺不光滑的现象。为了削弱干扰信号的影响,需对采样数据进行平滑处理。
对初始采集到的加速度数据进行截取,略去前后两端加减速工况的数据段,选取7.8s-11.2s的冲击数据段进行平滑处理。基于最小二乘法原理进行离散数据的直线滑动平均,其理论方法为:
式中,y为轮心加速度数据经平滑处理后的结果;x为轮心加速度采样数据;m为数据点数;2N+1为平均点数。
对加速度数据进行五点滑动平均,令N=2。处理前后结果对比如图3所示。其中虚线为原始信号,实线为经趋势项消除和平滑处理之后的数据。图4为图3的局部放大,可见,经平滑处理后的数据消除了高频噪声。
基于频域积分的轮心位移提取方法
在对加速度信号进行积分转化时,频域积分较于时域积分有其独特的优势。时域积分由于长周期误差信号的影响,积分结果易产生严重的漂移现象;且由于积分时使用逐步差值法,截断误差和舍入误差就不可避免。而频域积分的核心是将时域信号作傅里叶变换至频域内对其进行分析。在加速度数据的积分运算结果中,根据工程所需消除不需要的频率成分,再进行傅里叶逆变换得到时域信号。与时域积分相比,频域积分更加自由灵活且更为可靠。
1、频域积分方法
根据傅里叶变换公式,轮心加速度信号在任一频率的傅里叶分量可表达为
a(τ)=Aejωτ
式中,a(τ)为轮心加速度信号在频率ω的傅里叶分量;A为对应a(τ)的系数;j为虚数。
轮心初速度分量为0时,对轮心加速度信号分量的时间积分得轮心速度信号分量,即
式中,V(t)为轮心加速度信号在频率ω的傅里叶分量;V为对应V(t)的系数。
轮心初速度和初位移分量皆为0时,对轮心加速度信号的傅里叶分量两次积分可得轮心位移分量,即
式中,X(t)为轮心速度信号在频率ω的傅里叶分量;X为对应X(t)的系数。
于是,一次积分和两次积分在频域里的关系式分别为:
利用积分在频域里的关系式将所有不同频率的傅里叶分量进行运算,再经傅里叶逆变换即可得出轮心加速度数据相应积分后的轮心位移时域信号。
2、轮心实际行驶位移提取
为验证加速度频域积分法在获取轮心位移时是否可行,提出基于带通滤波的频域积分方式对预处理之后的右后轮心加速度数据进行积分变换。在积分后的傅里叶变换中进行带通滤波,通带频率范围之外的频率成分设置为零。为最大程度保留有用信息,设置通带的频率范围为0.2Hz-500Hz。
积分结果如图5所示,其中虚线为位移传感器实测位移,实线为加速度数据两次积分变换后得到的位移。结果可见,经积分所得的位移出现了较为严重的失真,表现为:零点向坐标轴负方向漂移了约20mm;在冲击过后和下次冲击到来之前的8.5s-10.5s之间,位移数据本该为零的平稳路段却积分出了约40mm的位移量,这与实际严重不符。
经过分析,初步断定是通带频率范围设置太广,低频趋势项没有得到有效消除,经两次积分后误差放大的结果。为了识别振动大小随频率的分布情况,运用Welch方法(平均周期图法)对轮心加速度数据的自功率谱密度函数进行求解,其幅频特性曲线如图6所示。
如图6所示,将加速度信号转移至频域来观察其相对幅值可看出,频率在2Hz-200Hz之外的加速度相对幅值近似于零,可认为该频率范围之外的加速度数据对之后的积分贡献不大,仅作为趋势项和噪声干扰而存在。为验证此假设的正确性,重新设定通带频率范围为2Hz-200Hz进行积分变换,将指定频率范围之外的数据置零,结果如图7所示,其中虚线为位移传感器实测位移,实线为加速度数据两次积分变换后得到的位移。
图7可见,修正设置参数后的加速度频域积分取得了良好的效果,误差范围得到了很好的控制。在车轮受到路缘冲击之后车身位移波动幅度较大,而此时轮心位移仅围绕零坐标轴上下小副波动,这与实际情况相符。图8所示为修正参数后积分结果与位移传感器实测数据对比的局部放大图。
分析图8局部放大图,冲击产生时,在弹簧压缩行程,积分所得轮心位移曲线紧跟实测位移曲线提升,同时达到峰值,峰值大小相差0.5mm;冲击产生瞬间,可认为车身在垂直地面方向没有运动,那么,此时的实测位移值即是车轮跳动值,积分所得与实测数据相差在2%以内。在弹簧回弹行程,积分所得位移曲线紧跟实测位移曲线下降,在弹簧回弹极值点,峰值大小相差9mm;实测位移值大于积分位移值约20%,这是冲击产生后弹簧回弹,车身开始向上浮动造成的,这种现象的存在说明理论计算结果与实际状况一致,验证了积分结果的合理性。
以上所述仅为本发明的较佳实施例而已,并不以本发明为限制,凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等,均应包含在本发明的保护范围之内。
- 还没有人留言评论。精彩留言会获得点赞!