一种改进的全封闭制冷压缩机转速的测量方法与流程
本发明涉及全封闭式制冷压缩机转速的测量技术领域,具体涉及算法应用、电流测量、电机测量、制冷系统、数据采集以及数字信号处理等领域,尤其是一种全封闭制冷压缩机转速的测量方法
背景技术:
在制冷系统中,压缩机作为系统核心部件,其转速的测量对整个系统具有十分重要的意义,它对系统的制冷量、效能比、温度控制等重要指标有着十分明显的影响。而对于绝大多数的制冷压缩机,其结构都是全封闭式的,故传统的直接测量法(如编码器)对压缩机本身都具有破坏性,已不再适用。现阶段常用的间接测量方法主要是基于压缩机外壳震动,经实验验证,基于振动的测量方法对安装底座的材料和测试环境要求较高,当安装底座的刚度较小时,外壳的大量振动能量会被底座吸收,致使传感器无法精确捕捉测量信号,且如果测试环境中有其他产生振动的设备,亦会对振动测量产生影响,以上原因导致该方法的测量精度不足。
技术实现要素:
为了克服已有全封闭制冷压缩机转速的测量方法的测量精度较低、环境抗扰性差和测量设备复杂的不足,本发明提供一种测量精度较高、环境抗扰性良好和测量设备简化的改进的全封闭制冷压缩机转速的测量方法。
本发明解决其技术问题所采用的技术方案是:
一种改进的全封闭制冷压缩机转速的测量方法,所述测量方法包括以下步骤:
(1)电流信号的采集:利用电流跟随型传感器以及高速数据采集卡,对电机供电电流进行采集;
(2)数据存储:利用LabView对经过A/D转换的数字信号进行采集、存储;
(3)基于Hilbert变换进行有效信号提取:针对采集的数据进行数字信号处理;
(4)频域转换:利用线性调频Z变换对信号进行处理,得到频域信号;
(5)转速提取:针对以上频域信号,对最大值进行提取,所得频率乘以60即为压缩机转速。
进一步,所述步骤(2)中,转换后的数据以EXCEL的形式保存起来;所述步骤(3)中,利用软件Matlab读取EXCEL数据,并进行数据处理。
再进一步,所述步骤(2)中,转换后的数据暂存在内存;所述步骤(3)中,把Matlab插件内嵌在LabView里面,对暂存在内存中的数据进行实时处理。
更进一步,所述步骤(3)中,首先采用巴特沃斯滤波器进行低通滤波,之后利用希尔伯特变换Hilbert变换进行供电频率处理,可有效去除50HZ供电频率。
所述步骤(3)中,Hilbert变换的滤波过程如下:
提取的电流信号Y以如下公式进行模拟:
Y=100sin(100πt)-5sin(98πt)+10sin(2πt)
第一项100sin(100πt)为供电电流的信号,第二项5sin(98πt)为转速频率信号,第三项10sin(2πt)为转差率信号;
设原信号为S(T),经过希尔伯特变换的信号为T(T),对信号做如下处理:将第一项100sin(100πt)信号变成了100V的直流信号,电流信号中50HZ已经滤掉,对此进行频谱分析,得到49HZ这个转速频率。
本发明的技术构思为:基于Hilbert变换电流提取技术的测量方法,此方法测量结构简单,对制冷系统影响小,且仅需使用价格十分便宜的电流跟随型传感器。并在对有效信号提取时,利用Hilbert变换成功滤掉供电电流,便于对有效频率进行提取。
本发明的有益效果主要表现在:
(1)对比直接测量的破坏性,该方法对系统影响小。
(2)相比于基于振动等现行常用方法,对环境的抗扰性强,稳定性高。
(3)相比于FFT、CZT等频率提取方法。
(4)利用Hilbert变换可以有效消除供电50HZ频率对有效频率的干扰。
(5)该方法安装简便,成本较低,测量速度快。
附图说明
图1是制冷系统的示意图,其中1为制冷压缩机;2为排气压力表3为冷凝器;4为蒸发器;5为吸气压力表;6为供电火线;7为电流传感器;8为供电零线。
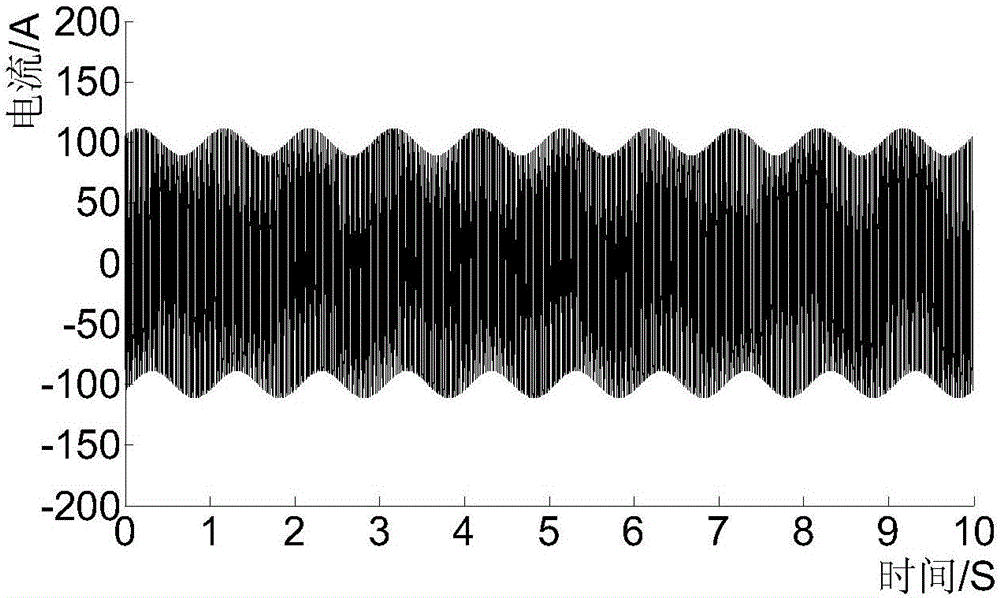
图2是仿真模型时域波形。
图3是数据处理后时域图。
图4是数据处理前仿真频域图。
图5是数据处理后仿真频域图。
图6是压缩机实采数据时域图。
图7是压缩机实采数据频域图。
具体实施方式
下面结合附图对本发明作进一步描述。
参照图1~图7,一种改进的全封闭制冷压缩机转速的测量方法,所述测量方法包括以下步骤:
(1)电流信号的采集:利用电流跟随型传感器以及高速数据采集卡,对电机供电电流进行采集;
(2)数据存储:利用LabView对经过A/D转换的数字信号进行采集、存储;
(3)基于Hilbert变换进行有效信号提取:针对采集的数据进行数字信号处理;
(4)频域转换:利用线性调频Z变换对信号进行处理,得到频域信号;
(5)转速提取:针对以上频域信号,对最大值进行提取,所得频率乘以60即为压缩机转速。
本实施例的全封闭制冷压缩机转速的测量方法,包括以下步骤:
(1)电流信号的采集:采集数据采用的是研华的PCI板卡,型号为PCI-1715U,板卡为高速采集卡,12位,500KS/s速度,远超采集需求。跟随型电流传感器为维博公司生产的WBI411S07,该传感器响应时间为15us,本实验系统的供电电流频率为50Hz,即周期为0.02s。整套系统的采集响应速度完全足够;
(2)数据存储:上位机通过PCI板卡和LabView软件对采样的模拟信号进行A/D转换,转换后的数据分两种数据存储方案:第一种,将数据以EXCEL的形式保存起来;第二种,将数据暂存在内存;
(3)数字信号处理:根据步骤(2)数据存储方式的不同,分两种途径读取数据:3.1、针对步骤二所述的第一种存储方式,利用软件Matlab读取EXCEL数据,并进行数据处理;3.2、针对步骤二所述的第二种存储方式,直接把Matlab插件内嵌在LabView里面,对暂存在内存中的数据进行实时处理,以达到实时测量转速的效果。上述两种方式的数据处理方法相同,首先采用最平的巴特沃斯滤波器进行低通滤波,之后利用希尔伯特变换Hilbert变换进行供电频率处理,可有效去除50HZ供电频率。
(4)频域转换:利用线性调频Z变换对信号进行处理,得到频域信号;
(5)转速提取:针对以上频域信号,对最大值进行提取,所得频率乘以60即为压缩机转速。
关于提取信号成分组成的证明:经过实验与分析,提取的电流信号可以以如下公式进行模拟:
Y=100sin(100πt)-5sin(98πt)+10sin(2πt)
其中的三个正弦函数的幅度值是根据经验比例模拟的,并非实际值,但三个幅值比例与真实值近似。
其中,第一项100sin(100πt)为供电电流的信号,因为供电电流为50HZ。所以为100πt,幅值选择100而不是220V,原因是我们再次只需要比例关系,故对所有三个系数同时除以2.2,以便分析。
第二项为转速频率信号,分析如下,制冷压缩机为异步电动机通过曲柄活塞机构带动进行吸排气,由于排气压力大于吸气压力,所以电动机在一个循环周期内负载是成周期变化的,进过分析,负载周期变化的规律近似正弦,频率即为自己转速频率,由于异步电动机的转速与负载相关,负载大时转速低,根据异步电动机的特征曲线,可以知道负载跟转速呈线性关系。而由于旋转磁场切割转子时会产生感生电动势,切割速度(即转差)越快,感生电动势越大,而感生电动势是供电电流始终成抵消状态,故第二项为负。由于是仿真,我们假设压缩机转动频率为49HZ,幅值为5,即为仿真函数的第二项。此项频率即为所需转速频率。
第三项为转差率信号,原理如下,由于旋转磁场切割转子,且始终比转子转速快,故我们可以假定转子不动,旋转磁场以1HZ(转差频率)转速旋转,则当旋转磁场与转子平行时,切割速度最快,所产生的感生电动势影响最为强烈。而当旋转磁场与转子垂直时,基本不切割转子,所以不产生感生电动势,故我们假设波动幅值是10,转差率为1HZ,以作仿真。
关于Hilbert变换的滤波原理说明:因为有效频率跟供电电流频率相距太近,而供电电流频率强度太大,故无法对转速频率进行提取。本发明提出一种基于Hilbert变换的数据处理方法,可以有效提取转速信号。
希尔伯特变换是一种数字信号处理手段,经过此种信号处理后,可以把时域信号投影到复数域中,投影后的信号,实数域为原信号,而虚数域则进行了-90度的相位移动。
根据数学模型Y=100sin(100πt)-5sin(98πt)+10sin(2πt)。
100sin(100πt)为主要内容,希尔伯特变换会对主要部分进行-90度相移而对次要部分影响不大。故经过希尔伯特变化后,100sin(πt)近似100cos(πt),而其他部分由于幅值较小,故希尔伯特变换对其影响较小。
我们知道三角函数有一个公式:sin2x+cos2x=1;
由此我们对采集信号做如下处理:设原信号为S(T),经过希尔伯特变换的信号为T(T),则我们对信号做如下处理:这样就将100sin(100πt)信号变成了100V的直流信号。结果如图3,可以看出电流信号中50HZ已经滤掉,对此进行频谱分析,就可以得到49HZ这个转速频率。
- 还没有人留言评论。精彩留言会获得点赞!