一种基于系数期望的杂波扩展相消方法与流程
本发明涉及外辐射源雷达领域,尤其涉及一种时域杂波抑制方法。
背景技术:
近年来,利用第三方辐射源作为照射源的外辐射源雷达因其绿色环保、隐蔽性好、抗干扰能力强、具有良好的反隐身能力等诸多优点逐渐成为了国内外的研究热点。外辐射源雷达自身不发射信号,需要接收直达波信号作为参考信号用于后续信号处理。因此,在雷达系统中需包含两类通道:接收直达波的参考通道和接收目标回波的监测通道。而通常选用的照射源均工作于连续波模式,监测通道不可避免的会接收到直达波及多径信号(后文中统称为多径杂波),这些多径杂波信号远强于目标回波。另一方面,大部分照射源均不是为了雷达设计的,信号的自模糊函数具有较低的峰值旁瓣比。这使得在计算参考信号和监测信号的互模糊函数时,目标的峰值会被多径杂波的旁瓣湮没,只有首先抑制多径杂波才能使目标凸显出来。因此,多径杂波抑制是外辐射源雷达信号处理的关键步骤之一。
现在已经有多种杂波抑制算法被提出,从抑制原理上可以分为时域滤波、空域滤波和频域滤波。时域滤波方法因其抑制能力强、对系统要求较低而在杂波抑制算法中占主导地位。在众多时域滤波方法中,基于最小二乘推导的杂波扩展相消算法(Extensive Cancellation Algorithm,ECA)因其抑制能力强、易于收敛等优点,近年来被广泛应用。为了获得较好的抑制效果,算法需要构建较大的杂波空间矩阵,增加了算法计算量,同时也对硬件存储空间提出了更高的要求。为了降低算法的运算消耗,扩展相消批处理算法(Extensive Cancellation Algorithm Batches,ECA-B)被提出。ECA-B算法将信号分段后每段分别使用ECA算法滤波,降低了杂波子空间的维度和最大运算储存空间消耗。同时通过分段处理增加了滤波器零陷宽度,降低了运算积累时间,算法在非平稳环境下具有更好的鲁棒性。但是滤波器零陷宽度由每段数据的积累时间决定,这意味着每段数据积累时间不能过短,限制了ECA-B算法的最大分段数。同时算法还会对低多普勒目标造成调制。滑窗扩展相消算法(Extensive Cancellation Algorithm Sliding,ECA-S)通过增加额外的滑窗单元来估计滤波器系数来改善上述问题。但是为了获得良好的抑制性能,需要新增加大量的滑窗单元,使算法整体计算量大幅提高。
随着外辐射源雷达技术的发展,外辐射源雷达的工程应用在近几年受到了越来越来的关注,而实时处理是其工程应用的前提。作为外辐射源雷达信号处理中计算量最大的步骤之一,时域杂波抑制的实时化决定了整个系统实时化工作的性能。通过上述的分析,现有的ECA系算法在实时化实现上均有各自的局限性,限制了杂波抑制算法实时化的性能。
技术实现要素:
针对上述提出的问题,本发明的目的是提供一种基于系数期望的杂波扩展相消方法。
本发明所提出的一种基于系数期望的杂波扩展相消方法(Extensive Cancellation Algorithm Expectation,ECA-E),其特征在于,包含以下步骤:
步骤一:将参考信号Sref和监测信号Ssurv平均分成b段,第i段参考信号和监测信号分别为:和其中,N为监测信号长度,R为参考信号额外所需的样本数,且R不小于需抑制的距离元K;
步骤二:将分段后的参考信号按统一的规则构造杂波矩阵,则第i段参考信号Srefi构造的杂波矩阵表示为:Ci=B[Srefi DSrefi D2Srefi…DK-1Srefi]。其中,B为关联矩阵,用于提取矩阵的最后行元素,定义为D为移位矩阵,定义为
步骤三:分段用最小二乘估计杂波矩阵系数,第i段数据杂波矩阵系数θi估计为
步骤四:对每段数据估计的杂波矩阵系数求期望
步骤五:返回至每段数据进行杂波抑制后,将每段数据按顺序拼接起来,获得整段数据的杂波抑制结果。
步骤四中求参数期望时的权值可以进一步简化:当参考信号为平稳信号,信号功率近似不变时,均匀分段后每段信号的能量近似相等,因此期望求取表达式可以化简为采取简化后表达式进行杂波抑制的方法称为ECA-ES(Simplified ECA-E)。
ECA-E和ECA-ES算法拥有优秀的静态杂波抑制能力,而对动杂波抑制能力较差,在实际应用中,可以与扩展相消批处理算法(Extensive Cancellation Algorithm Batches,ECA-B)结合,同时抑制静态杂波和强动杂波,获得更好的杂波抑制效果。这种二阶滤波方案分别称为ECA-E&B和ECA-ES&B,包含以下步骤:
步骤一:采用ECA-E或ECA-ES对前K个距离元的静态杂波抑制,并保留算法分段结构;
步骤二:应用ECA-B算法对直达波附近的KB个距离元进行杂波抑制,算法分段结构与步骤一相同;
步骤三:将每段数据按顺序拼接起来,获得整段数据的杂波抑制结果。
基于系数期望的杂波扩展相消方法(Extensive Cancellation Algorithm Expectation,ECA-E)采用与扩展相消批处理算法(Extensive Cancellation Algorithm Batches,ECA-B)相同的方式将杂波矩阵和监测信号分段后,对参考信号延时处理构造相同维度的杂波矩阵,每段信号分别采用最小二乘法估计杂波系数;对每段信号估计的杂波系数求期望获得整段数据的杂波系数;将统一的杂波系数返回至每段数据进行杂波抑制;该方法对静态杂波有优秀的抑制能力,在实际应用中可以与ECA-B算法结合,同时抑制静态杂波和强动杂波,获得更好的杂波抑制效果。
本发明的优势在于:算法在保证杂波抑制性能的基础上,通过分段处理使算法具有更好的并行架构,能够大幅降低每部分的计算消耗。并行运算时能明显提高运算效率,进而提高整个外辐射源雷达系统实时化性能。
附图说明
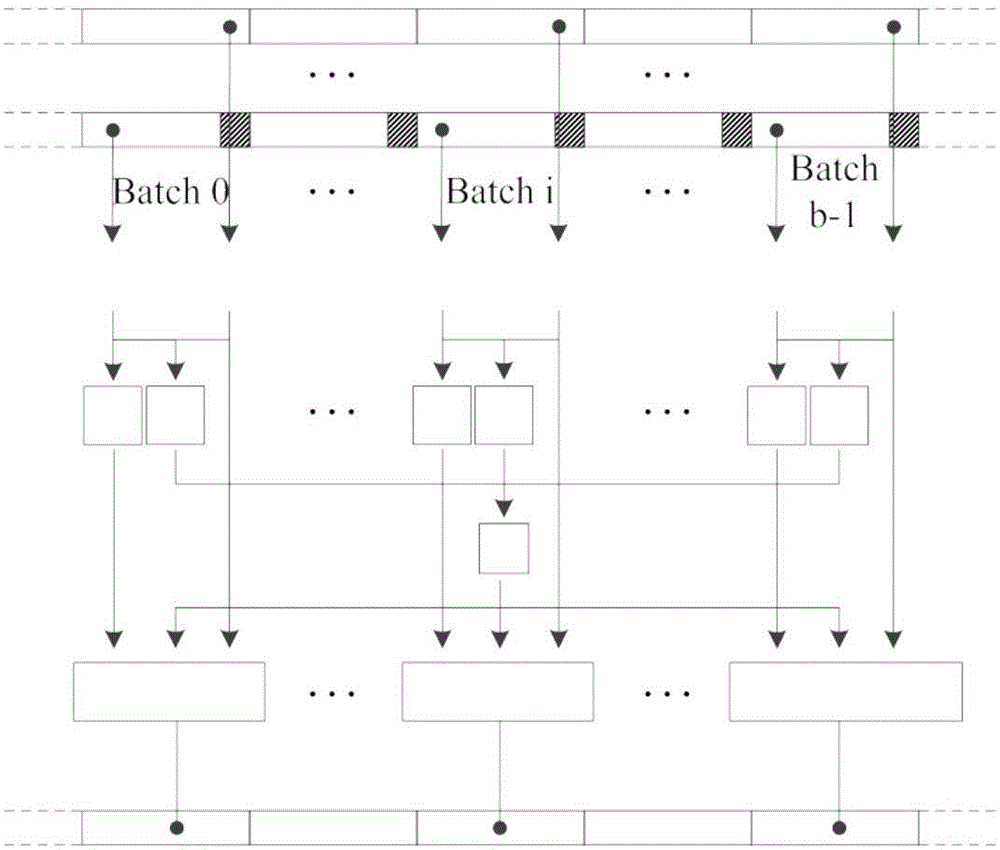
图1是本发明提供的ECA-E和ECA-ES方法结构框图。
图2是本发明提供的ECA-E&B和ECA-ES&B方法结构框图。
图3是本发明提供的方法在距离维上抑制性能的对比图。
图4是本发明提供的方法在多普勒维上抑制性能的对比图。
图5是本发明本发明实施例中未经过杂波抑制的互模糊函数图。
图6是本发明本发明实施例中ECA-E抑制后的互模糊函数图。
图7是本发明本发明实施例中ECA-ES抑制后的互模糊函数图。
图8是本发明本发明实施例中ECA-E&B抑制后的互模糊函数图。
图9是本发明本发明实施例中ECA-ES&B抑制后的互模糊函数图。
具体实施方式
下面以具体实施方式结合附图对本发明做进一步说明。
本实施例中,选用的外辐射源为调频广播信号,系统采样率为500kHz,每次处理的相干积累时间均为1s。
如图1所示,本发明所提出的一种基于系数期望的杂波扩展相消方法(ECA-E)包含以下步骤:
步骤一:将参考信号Sref和监测信号Ssurv平均分成b段,第i段参考信号和监测信号分别为:和其中,N为监测信号长度,R为参考信号额外所需的样本数,且R不小于需抑制的距离元K;
步骤二:将分段后的参考信号按统一的规则构造杂波矩阵,则第i段参考信号Srefi构造的杂波矩阵表示为:Ci=B[Srefi DSrefi D2Srefi…DK-1Srefi]。其中,B为关联矩阵,用于提取矩阵的最后行元素,定义为D为移位矩阵,定义为
步骤三:分段用最小二乘估计杂波矩阵系数,第i段数据杂波矩阵系数θi估计为
步骤四:对每段数据估计的杂波矩阵系数求期望
步骤五:返回至每段数据进行杂波抑制后,将每段数据按顺序拼接起来,获得整段数据的杂波抑制结果。
当使用ECA-ES算法时,步骤四可以化简为
ECA-E&B和ECA-ES&B算法的结构如图2所示,包含以下步骤:
步骤一:采用ECA-E或ECA-ES对前K个距离元的静态杂波抑制,并保留算法分段结构;
步骤二:应用ECA-B算法对直达波附近的KB个距离元进行杂波抑制,算法分段结构与步骤一相同;
步骤三:将每段数据按顺序拼接起来,获得整段数据的杂波抑制结果。
本发明的性能可以通过与现有算法的比较进一步说明。
本实施例中,对比算法为ECA、ECA-B和ECA-S。ECA-B、ECA-S、ECA-E和ECA-ES分段数分别为bECA-B、bECA-S、bECA-E和bECA-ES。ECA-S算法的滑窗单元长度为s。根据文献(Sliding extensive cancellation algorithm for disturbance removal in passive radar,in IEEE Transactions on Aerospace and Electronic Systems,vol.52,no.3,pp.1309-1326,June 2016)中所提出的分析方法,当同样抑制K距离元的杂波信号时,杂波抑制部分的计算量C2(K,Ny)均相同,各算法计算量的区别主要体现在估计滤波器系数部分的计算量C1(K,Nx)上。其中Nx和Ny分别为用于滤波器系数估计和滤波操作的数据长度。
表1比较了各算法的C1(K,Nx)。尽管ECA-E和ECA-ES算法计算量相对于ECA和ECA-B整体上略有增加,但是算法通过将数据大量分段,使算法具有更好的并行结构,能够大幅降低每部分的计算消耗,提高运算效率。ECA-S算法虽然也能与ECA-E和ECA-ES算法拥有相似的分段能力,但是为了保证抑制性能,需要大量的滑窗单元。算法运算量无论是整体上还是每部分的都远远大于ECA-E和ECA-ES算法。ECA-E&B算法计算量为ECA-E算法和ECA-B算法计算量之和。在ECA-E&B算法中,ECA-B算法抑制的距离元远少于ECA-E算法,且经过大量分段,ECA-B算法在每部分新增的计算量相对于ECA-E算法可以被忽略。因此ECA-E&B算法计算量与ECA-E算法相似。ECA-ES&B算法也是一样,计算量与ECA-ES算法相似。
表1各算法C1(K,Nx)比较
引入杂波抑制比(Clutter Attenuation,CA)来评估算法抑制性能,CA定义为Pin和Pout分别代表滤波器的输入信号和输出信号能量。
本实施例中参考信号为仿真生成的调频广播信号,信噪比为70dB。滤波器参数为bECA-B=10、bECA-S=20、bECA-E=bECA-ES=50,ECA-S算法的滑窗长度s=5e4。当抑制前10个距离元杂波时,各算法在距离维和多普勒维上的CA曲线分别如图3和图4所示。从图中可以看到,ECA-E和ECA-ES算法对静态杂波拥有优秀的抑制能力,抑制性能与现有算法基本相同,但是对动杂波抑制能力较弱。
本发明实施例的效果可通过空中目标探测的外场实验进一步说明。
本实施例中,分段数bECA-E=bECA-ES=50,信号长度N=5e5,R=K=200。在ECA-E&B和ECA-ES&B算法中,ECA-E和ECA-ES算法部分参数不变,KB=4。
图5是某段数据杂波抑制前的互模糊函数图,目标被强多径杂波的旁瓣湮没。
图6-9分别给出了使用ECA-E、ECA-ES、ECA-E&B和ECA-ES&B算法滤波后的互模糊函数图。ECA-E和ECA-ES算法滤波后,强静态杂波被抑制,目标凸显出来,但是近场仍存在很强的动杂波,影响了近距离目标的探测性能。而ECA-E&B和ECA-ES&B算法能够获得较为干净的互模糊函数图,近距离目标得以显现。
本文中所描述的具体实施例仅仅是对本发明精神作举例说明。本发明所属技术领域的技术人员可以对所描述的具体实施例做各种各样的修改或补充或采用类似的方式替代,但并不会偏离本发明的精神或者超越所附权利要求书所定义的范围。
- 还没有人留言评论。精彩留言会获得点赞!