间接测定植物表面PM2.5的干沉降速率的方法与流程

本发明涉及一种间接测定植物表面PM2.5的干沉降速率的方法，属于植物表面物理性质领域。
背景技术：
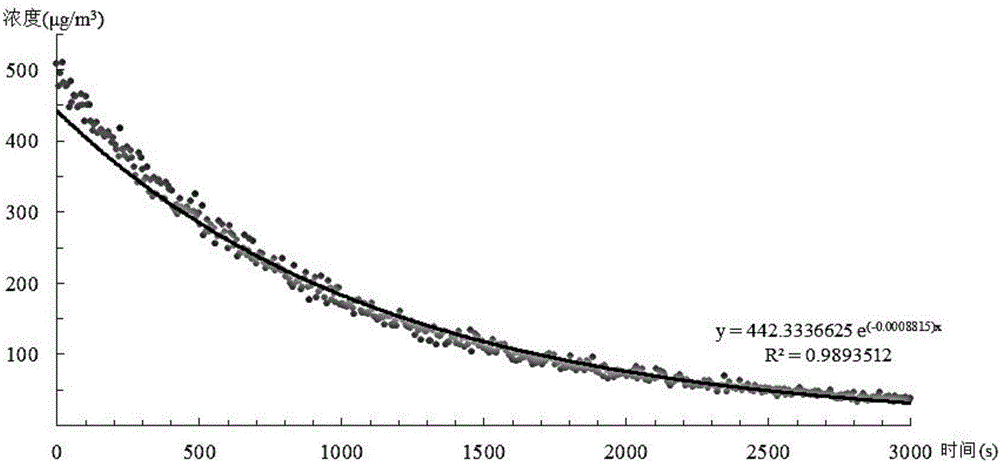
：在空气污染日趋严重的今天，越来越多的关注聚焦在大气污染问题上。大气中直径小于或等于2.5微米的细颗粒污染物，简称为PM2.5，因其传播距离远，对人体健康影响大，已成为大气污染防控的首要目标。测定PM2.5在植物叶片上的干沉降速率，为雾霾治理和污染防控提供科学依据，已经迫在眉睫。研究表明，干沉降(drydeposition)是植被净化大气颗粒物的主要机制。植物的滞尘能力可以用单位面积植物叶片上PM2.5的干沉降通量(F)来表示：F(μg/m2/hr)＝Vd×C式(1)式中Vd为干沉降条件下植物叶片吸滞PM2.5的速率(m/hr)，随植物种类及环境因素的不同而不同；C为当地大气中PM2.5本底浓度(μg/m3)。经过对现有技术的大量检索后发现，目前测定植物干沉降速率Vd的主要方法有洗脱法和风洞实验法。但是洗脱法仅仅适合不溶性的粗颗粒，同时由于称量量非常微小，称量中容易产生累计误差，不适用于细小的PM2.5颗粒物干沉降速率的测量；而风洞实验法用NaCl或KNO3为示踪物模拟大气中的颗粒物，其粒径约在0.8μm，不能代表大气中PM2.5的真实粒径，且实验成本很高，实验条件要求较为苛刻，操作难度较大。技术实现要素：针对现有技术中的缺陷，本发明的目的是提供一种间接式测定植物表面PM2.5的干沉降速率的方法。本发明是通过以下技术方案实现的：本发明提供了一种间接测定植物表面PM2.5的干沉降速率的方法，其包括如下步骤：S1：制备PM2.5模拟颗粒物；S2：确定测定过程中烟雾箱内PM2.5的浓度范围和测定时长；S3：确定所述浓度范围和测定时长内烟雾箱体中PM2.5的浓度随时间的指数衰减变化规律，并建立数学模型确定衰减速率常数j；S4：确定所述浓度范围和测定时长内含有叶片的烟雾箱箱体中PM2.5的浓度随时间的指数衰减变化规律，并建立数学模型确定衰减速率常数k；S5：根据获得的两个衰减速率常数j、k的数据，推导出所测试叶片样品对PM2.5的干沉降速率Vd计算公式，如式I所示，其中V为烟雾箱箱体容积，LA为测试叶片样品叶面积；作为优选方案，所述PM2.5模拟颗粒物为平均粒径为2.5μm的金刚石微粉。作为优选方案，步骤S2中验室模拟用PM2.5颗粒物的浓度范围为20～400μg/m3，测定时长为1000秒。作为优选方案，步骤S3具体包括如下操作：用纯净氮气冲洗烟雾箱箱体内壁，当箱体内的PM2.5浓度下降到10μg/m3以下并稳定时，用洗耳球吹入PM2.5模拟颗粒物，使箱体内PM2.5浓度达到400μg/m3。此时利用Grimm32通道粒径谱仪，每6秒测定并记录1次箱体内PM2.5的浓度，测定时长为1000秒。测定之后利用matlab软件将箱体内PM2.5浓度随时间的变化规律拟合为指数衰减模型C(t)＝C0·exp(-j·t)，其中C(t)为在t时刻PM2.5的浓度，C0是PM2.5的起始浓度，j为衰减速率常数，通过拟合计算而得到。作为优选方案，步骤S4具体包括如下操作：将刚采下的叶片用流动水冲洗三遍并自然晾干后，悬挂于烟雾箱箱体内的挂钩上，盖上箱盖，用纯净氮气冲洗箱体内壁，当箱体内的PM2.5浓度下降到10μg/m3以下并稳定时，用洗耳球吹入PM2.5模拟颗粒物，使箱体内PM2.5浓度达到400μg/m3。此时利用Grimm32通道粒径谱仪，每6秒测定并记录1次箱体内PM2.5的浓度，测定时长为1000秒。测定之后利用matlab软件将箱体内PM2.5浓度随时间的变化规律拟合为指数衰减模型C(t)＝C0·exp(-k·t)，其中C(t)为在t时刻PM2.5的浓度，C0是PM2.5的起始浓度，k为衰减速率常数，通过拟合计算而得到。作为优选方案，所述烟雾箱包括：不锈钢外壳、密闭罐体、变速风扇、温控探头、环形空气冲洗管路、空气进气口、罐体顶盖、密封固定螺栓、预留检测口、操作面板、配电箱、内外压力平衡装置、真空泵，密闭罐体位于不锈钢外壳内，变速风扇、环形空气冲洗管路从下至上依次位于密闭罐体内，空气进气口、罐体顶盖、操作面板都固定在不锈钢外壳的顶端上，预留检测口位于罐体顶盖上，罐体顶盖和不锈钢外壳之间通过密封固定螺栓固定，真空泵位于不锈钢外壳内且位于密闭罐体的侧面。具体可参见专利ZL201510093611.X。与现有技术相比，本发明具有如下的有益效果：与传统测定法相比，本发明通过观测数据拟合得到的公式进行计算，可极大减小系统误差，提高测定的精确度，并且实验成本低，实验耗时少，操作更加简便易行。附图说明通过阅读参照以下附图对非限制性实施例所作的详细描述，本发明的其它特征、目的和优点将会变得更明显：图1为实施例中符合要求的金刚石微粉不同粒径颗粒的个数及浓度分布图；图2为实施例中空白烟雾箱内空气PM2.5浓度随时间变化的趋势图；图3为实施例中不同初始浓度下烟雾箱内PM2.5浓度的自然对数值随时间的变化图(各回归方法中的截距即初始浓度)；图4为浓度在400～20μg/m3范围内烟雾箱内PM2.5浓度的自然对数值随时间的变化图；图5为浓度在400～20μg/m3范围内，时间控制在1000s内的箱体内PM2.5浓度的自然对数值随时间的变化图；图6为烟雾箱内PM2.5浓度的指数衰减函数图；图7为新获得系数代替原拟合方程系数构成的新直线方程(各回归方法中的截距即初始浓度)；图8为实施例中试样和空白对照的PM2.5浓度的指数衰减函数图；图9带有无患子叶片的烟雾箱内PM2.5浓度随时间变化的趋势和拟合函数图；图10不同时间间隔对应的无患子叶片PM2.5沉降速率图。具体实施方式下面结合具体实施例对本发明进行详细说明。以下实施例将有助于本领域的技术人员进一步理解本发明，但不以任何形式限制本发明。应当指出的是，对本领域的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干变形和改进。这些都属于本发明的保护范围。实施例1本实施例涉及一种间接测定植物表面PM2.5的干沉降速率的方法，其包括如下步骤：1、实验室模拟用PM2.5颗粒物的制备为确保实验室模拟用PM2.5颗粒物粒径符合试验要求，我们依次对购买不同粒径的金刚石微粉做预实验，通过Grimm1109粒径谱仪的测定，得到符合试验要求的金刚石微粉。如图1所示，备选用金刚石微粒的质量浓度主要集中分布在颗粒直径2.5μm处，符合试验要求。2、实验室模拟用PM2.5颗粒物的浓度范围的确定及实验持续时间的确定2.1实验室模拟用PM2.5颗粒物的浓度范围的确定烟雾箱体内部的表面积为一固定值，根据空气动力学原理得知，在有风扇搅动情况下，密闭容器内的颗粒物的浓度随时间变化的趋势符合指数衰减类型。为了确定PM2.5颗粒物的浓度取值范围，制备12组不同浓度的金刚石微粒(69～1212μg/m3，空气中常见的浓度取值)，并记录了对应的PM2.5颗粒物浓度随时间变化的数据，经过线性拟合发现，其趋势均符合指数衰减类型(如图2)，为方便进一步研究，现将各组PM2.5浓度值取自然对数，对处理后的数据进行图像分析处理，结果如图3所示。由图3可知，每一组经数据处理后，其新构成的图像接近于直线，对每一组的图像进行拟合，可得到相应的拟合直线。现将各组直线按照其与y轴的截距从大到小进行排列，如表1所示。表1不同浓度下的回归方程和相应的R2值在不同的浓度下，拟合所得方程的系数在-0.0010153～-0.0007972之间浮动，虽然该12个系数数值相对集中，但最大值与最小值之间仍相差了20％左右，不利于对缸体的适宜参数的确定，故需要对数据进行一定的筛选。根据图4和图5可以发现，当纵坐标大于或接近于6(对应PM2.5浓度约为400μg/m3)时，其数据点大部分偏离了回归方程，而位于其上方；当纵坐标位于6和5(对应PM2.5浓度约为150μg/m3)之间时，虽有若干点偏离回归方程而位居其上，但其个数只占总体个数较小的部分；当纵坐标小于3(对应PM2.5浓度约为20μg/m3)时，数据点之间的波动明显，离散程度较大。对于经过筛选后的各组浓度点进行重新拟合，按照其与y轴的截距从大到小进行排列，如表三所示。新拟合所得方程的系数在-0.0011117～-0.0008368之间浮动，这12个新系数数值比之前的数值更为集中，但最大值与最小值之间仍相差了20％左右。另外，对原初始浓度大于400μg/m3的三组数据拟合所得方程的系数分别为-0.0010161、-0.0008591和-0.0008368，相互之间比较离散，且原初始浓度为1212μg/m3和596μg/m3较为远离400μg/m3这个浓度，在数据进一步处理时可能有很大的影响，因此将其筛除。其余数据需要通过控制时间的手段以求得到更好的试验效果。表2浓度在400～20μg/m3范围内的回归方程和相应的R2值2.2实验持续时间的确定持续时间的确定首先考虑之前确定的浓度降低至20μg/m3所需的时间，一般控制在600～3000s之内较为适宜，但是根据图3和图4可以发现，当时间超过1200s之后，各数据点之间虽然比浓度低于20μg/m3时出现的离散情况要好，但都或多或少出现了一定程度的离散现象，为了不影响数据的精确度和准确性，现只选取各组数据的前1000s，对筛选后的各组数据我们进行回归方程的拟合，如图4所示。对于经过第二次筛选后的各组浓度点进行重新拟合，按照其与y轴的截距从大到小进行排列，如表3所示。新拟合所得方程的系数在-0.0012857～-0.0009677之间浮动，这10个新系数数值比之前的数值更为集中，虽然最大值与最小值之间仍相差了20％左右，但是其余8个系数明显集中。3、烟雾箱内PM2.5浓度随时间衰减规律确定对于烟雾箱内PM2.5的浓度随时间的衰减规律确定，参考表3所拟合得到的回归方程，去除异常的最大值和最小值，对其余系数求平均值，可得到新的系数j＝-0.0010618。根据新获得系数，还原得到该烟雾箱内PM2.5浓度的指数衰减函数，如图6所示。依据每组的不同初始浓度，将新得到的系数替换原来拟合的直线的系数，得到图7。表3浓度在400～20μg/m3范围内，时间控制在1000s内的回归方程和相应的R2值4、含有待测叶片的烟雾箱内PM2.5浓度随时间衰减规律确定(以无患子为例)按照步骤S4所述，将无患子叶片经处理后置于烟雾箱进行测定，并记录相关数据，将得到的若干数据点进行拟合，得到如图8所示。5、所测叶片对PM2.5的干沉降速率Vd的推导(以无患子为例)5.1间接法测定叶片滞尘量公式的推导：取任意在测定范围内的t时刻，则t时刻所对应的含有试样的气溶胶气候箱缸体内部PM2.5浓度为：z(t)=C0×ekt式中，C0为初始浓度，k为带有无患子样品的烟雾箱内PM2.5浓度的衰减速率常数。则经过Δt时间后，含有试样的气溶胶气候箱缸体内部PM2.5浓度为：z(t+Δt)=C0×ek(t+Δt)为了使空白对照的气溶胶气候箱缸体内部PM2.5浓度与z(t)的浓度相同，则需令y(t′)＝z(t)，可得：t′=kt/j式中，j为空白对照的烟雾箱内PM2.5浓度的衰减速率常数。则经过Δt时间后，空白对照的气溶胶气候箱缸体内部PM2.5浓度为：y(t′+Δt)＝C0×ej(t+Δt)＝c0×ekt+j·Δt根据沉降速率的计算公式可以得到如下等式：Vd(t)=y(t′+Δt)-z(t+Δt)z(t)·Δt·VLA=C0×ekt+j·Δt-C0×ek(t+Δt)C0×ekt·Δt·VLA=(ej·Δt-ek·Δt)·VLA·Δt]]>式中，LA为测试树种的叶面积，V为烟雾箱的体积。5.2叶片滞尘量公式中的时间间隔Δt的确定根据上述推导可知：式中，系数j只与对于烟雾箱内部的性质和表面积有关系，而且由于每组实验中特定测试树种的叶片及叶面积LA都已经确定，所以系数k的数值也是确定的，烟雾箱的体积V也为一固定值，所以影响沉降速率结果大小取决于测试时间间隔。我们将测试无患子所得数据和空白气溶胶气候箱测得的数据进行拟合，可以得到图9，通过计算可知k＝-0.0015861，系数j＝-0.0010618，用叶面积仪可测得所用无患子叶面积为791.2541cm2，烟雾箱体积为0.4m3。将以上各系数带入式1中。对于时间间隔，分别取1000s、100s、10s、1s、0.1s、0.01s、0.001s、0.0001s，计算得到的干沉降速率Vd的数值，如图10所示。由图可知，当时间间隔在1000～10s区段内时，沉降速率的数值随时间间隔的缩小而增大，当时间间隔在10～0.0001s区段内，沉降速率的数值变化基本稳定不变。表4不同时间间隔对应的无患子叶片PM2.5沉降速率由表4可以发现，时间间隔越大，导致沉降速率的数值越偏小，但当时间间隔小于10s时，沉降速率数值基本保持恒定。同时考虑到数值的精准性和实际操作的可行性，可以将时间间隔控制在1～10s范围内。本实验建议时间间隔可取为1s，则Vd计算公式则可进一步简化为：以上对本发明的具体实施例进行了描述。需要理解的是，本发明并不局限于上述特定实施方式，本领域技术人员可以在权利要求的范围内做出各种变形或修改，这并不影响本发明的实质内容。当前第1页1 2 3