一种多翼离心风机及其分组设计方法与流程

本发明涉及气体动力学领域，尤其涉及一种多翼离心风机及其分组设计方法。

背景技术：

与常规的后向离心风机相比，多翼离心风机具有压力系数高、流量系数大、结构紧凑等优点，但也存在流动分离严重、效率低、能源浪费巨大等缺点，因此，如何消除或缓解流动分离现象、降低流动损失，对提高多翼离心风机气动性能、拓展多翼离心风机应用范围、发展节能环保型产品具有至关重要的作用。

目前，制约多翼离心风机性能大幅度提高的瓶颈是集流器、叶轮和蜗壳优化设计方法，国内外学者针对上述问题提出了诸多有效改进措施。温选锋等研究了椭圆形集流器的影响，周水清等研究了偏心集流器的偏心距和偏心角对风机性能的影响，发现较佳参数组合的集流器可以有效提高风机性能；罗嘉陶等研究了翼型叶片尾缘切割方式对多翼离心风机性能的影响，发现沿圆周线方向切除的翼型叶片具有较大的风量和全压，王湛研究了圆弧叶片型线对风机性能的影响，结果表明双圆弧叶片性能优于单圆弧叶片；Han等采用神经网络算法，刘小民等采用仿生技术，对蜗舌形状进行了优化，这些方法均有利于改善蜗舌附近的流动状况。

上述研究工作对多翼离心风机通流部件设计具有一定的指导意义。然而，这些工作大多侧重于风机单个部件的改进或优化，未能细致考虑动静部件尤其是叶轮与蜗壳间的匹配情况，限制了风机效率的进一步提高。事实上，受结构尺寸的限制，多翼离心风机大多数没有扩压器，叶轮与蜗壳之间的非轴对称影响非常明显，基于真实流动准确模拟的多翼离心风机系统综合设计研究还较为匮乏。

技术实现要素：

本发明要解决的技术问题是提供一种多翼离心风机及其分组设计方法，风机能够降低流动分离程度，提高效率，明显改善气动性能，设计方法能够降低计算量并具有较高的可靠性。

为了实现上述目的，本发明所采取的技术方案是：一种基于分组模型及仿生蜗舌的多翼离心风机，包括蜗壳、设置在蜗壳内的叶轮和蜗舌以及设置在蜗壳侧面的集流器，其特征在于：所述叶轮包括轮盘、轮盖和叶片，所述叶片为双圆弧形，叶片的进口安装角β₁为75°～90°，叶片的出口安装角β₂为160°～180°，叶片的进口半径和出口半径分别为160mm和202mm，叶片的两圆弧交接位置R_f为180～195mm，叶片的两圆弧交接位置的安装角为β_f为90°～120°，叶片的两圆弧交接位置R_f处于叶片中间靠近出口的位置，且从叶轮进口起的第一圆弧半径大于第二段圆弧半径；所述蜗壳由四段光滑的圆弧片连接构成，所述圆弧片以等边基方的四角为中心，蜗壳宽度、集流器宽度和叶轮轴向长度的比值为1.31:0.26:1；所述蜗舌为基于长耳鸮翼型前缘剖面型线的仿生结构。

进一步，所述叶片的进口安装角β₁为81.72°，叶片的出口安装角β₂为180°，叶片的两圆弧交接位置R_f为187.76mm，叶片的两圆弧交接位置的安装角为β_f为95.17°。

进一步，所述蜗舌为长耳鸮翼型前缘剖面型线前缘的6.5％。

多翼离心风机的设计方法：多翼离心风机包括蜗壳、设置在蜗壳内的叶轮和蜗舌以及设置在蜗壳侧面的集流器，依次对叶轮、蜗壳和蜗舌进行分组改进设计；

叶轮的改进：所述叶轮包括轮盘、轮盖和叶片，所述叶片为双圆弧形，首先固定叶片的进口安装角β₁和出口安装角β₂，采用单通道计算模型通过改变两圆弧交接位置R_f和叶片的两圆弧交接位置的安装角为β_f获得不同形状的双圆弧曲线，然后调整叶片的进口安装角β₁和出口安装角β₂，确定进口安装角β₁的变化范围75°～90°，出口安装角β₂的变化范围为160°～180°，最后，采用均匀设计方法在上述设计空间内进行试验设计，基于均匀设计表U31(31³⁰)，选出31个具有代表性的叶轮样本，并采用CFD数值模拟方法计算出不同形状的叶轮的效率；

蜗壳的改进：采用等边基方法对蜗壳型线重构设计，先根据设计参数确定等边基方，再以等边基方的四角为中心，用四段光滑连接的圆弧片构成蜗壳型线，此外，考虑到集流器与叶轮的轴向间隙较大，将蜗壳宽度、集流器宽度和叶轮轴向长度的比值设计为1.31:0.26:1，以满足集流器与叶轮的轴向匹配，最后将所述叶轮与蜗壳进行组合，进行整机CFD计算；

蜗舌的改进：提取长耳鸮翼型前缘剖面型线并采用Birnbaum-Glauert函数对中心线拟合：

式中：z_c为中弧线坐标；η＝x/c为弦坐标比；x为弦向坐标；z_c(max)为最大弧度坐标；c为翼型弦长；S_n为待定系数，翼型厚度拟合公式为：

式中：z_t为厚度；z_t(max)为最大厚度；A_n为待定系数，式(1)-(2)中的待定系数为：

n＝1时，S_n＝3.9362，A_n＝-29.4861

n＝2时，S_n＝-0.7705，A_n＝66.4565

n＝3时，S_n＝0.8485，A_n＝--59.8060

n＝4时，A_n＝19.0439；

将上述拟合所得的蜗舌先与蜗壳匹配后再与叶轮相结合，进行三维整机CFD计算；

最后将计算结果和实验结果进行对比验证计算模型的可靠性。

采用上述技术方案所产生的有益效果在于：本发明的蜗舌采用仿生设计，能够有效缓解蜗舌处的气体流动分离现象，减少能耗损失；叶轮的叶片采用四自由度的双圆弧形，能够有效提高风机效率；蜗壳由四段光滑的圆弧片连接构成，能够与双圆弧形的叶片和长耳鸮翼型的蜗舌完美匹配，消除蜗舌上方的旋涡、改善蜗舌与叶轮间的流动情况，从而提高风机效率；多翼离心风机的设计方法采用设计参数分组的方法，能够降低计算量并具有较高的可靠性。

附图说明

下面结合附图和具体实施方式对本发明作进一步详细的说明。

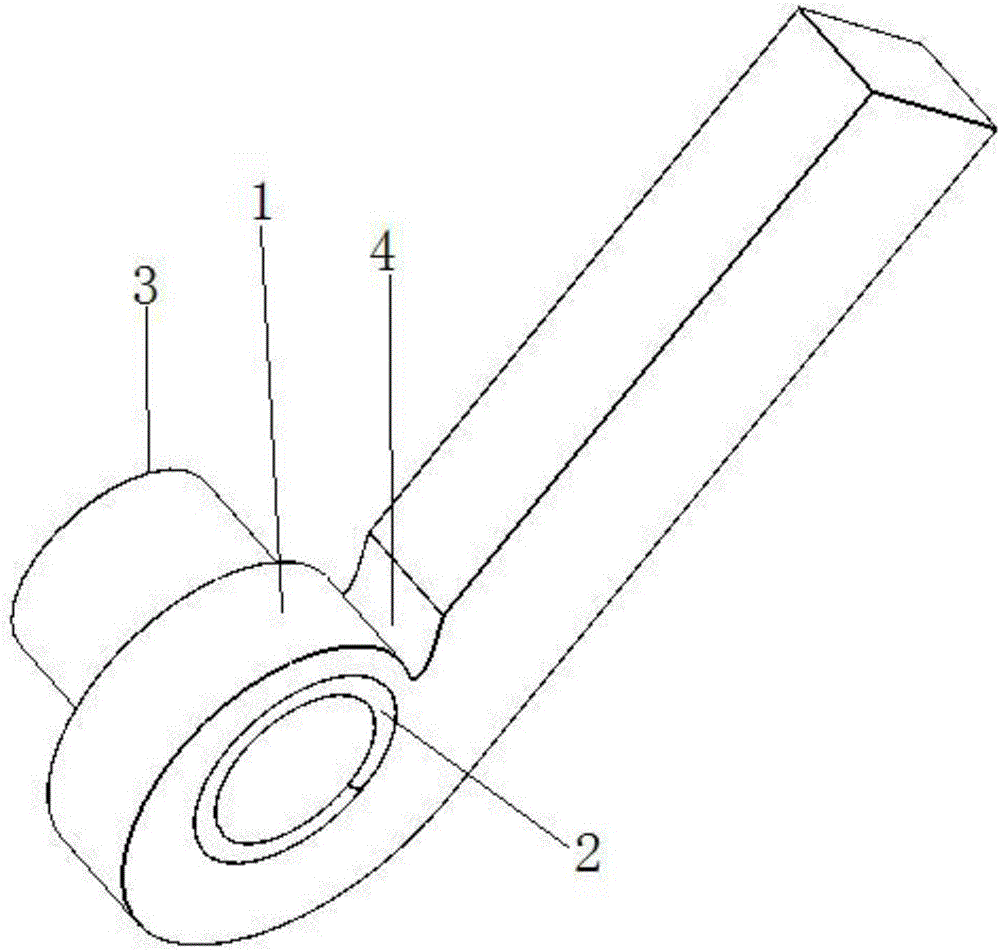
图1是本发明多翼离心风机计算流域的立体结构图。

图2是本发明叶片的二维结构示意图。

图3是改进后的四段圆弧蜗壳和仿生蜗舌的组装结构图。

图4是不同R_f和β_f组合所得的叶轮效率计算结果图。

图5是原始叶轮内相对速度流线图。

图6是双圆弧形叶片的叶轮内相对速度流线图。

图7是采用原始叶轮和原始蜗壳状态下的原始风机蜗壳内绝对速度流线图。

图8是采用双圆弧形叶片的叶轮和原始蜗壳状态下蜗壳内绝对速度流线图。

图9是原始叶轮和原始蜗壳状态下的原始风机蜗壳内的静压云图。

图10是采用双圆弧形叶片的叶轮和原始蜗壳状态下蜗壳内的静压云图

图11是双圆弧形叶片的叶轮与改进蜗壳组合下的风机蜗壳内的绝对速度流线图。

图12是双圆弧形叶片的叶轮与改进蜗壳组合下的风机蜗壳内的静压云图。

图13是采用双圆弧形叶片的叶轮与仿生蜗舌后的风机蜗壳内的绝对速度流线。

图14是采用双圆弧形叶片的叶轮与仿生蜗舌后的风机蜗壳内的静压云图。

图15是采用双圆弧形叶片的叶轮与仿生蜗舌的风机与原始风机的性能曲线对比图。

图中：1、蜗壳 2、叶轮 3、集流器 4、蜗舌 5、圆弧片。

具体实施方式

参看附图1和2，本发明一个具体实施方式的结构中包括蜗壳1、设置在蜗壳1内的叶轮2和蜗舌4以及设置在蜗壳侧面的集流器3，所述叶轮2包括轮盘、轮盖和叶片，所述叶片为双圆弧形，叶片的进口安装角β₁为81.72°，叶片的出口安装角β₂为180°，叶片的进口半径和出口半径分别为160mm和202mm，叶片的两圆弧交接位置R_f为187.76mm，叶片的两圆弧交接位置的安装角为β_f为95.17°，叶片的两圆弧交接位置R_f处于叶片中间靠近出口的位置，且从叶轮进口起的第一圆弧半径大于第二段圆弧半径；

所述蜗壳1由四段光滑的圆弧片5连接构成，所述圆弧片5以等边基方的四角为中心，蜗壳1宽度、集流器3宽度和叶轮2轴向长度的比值为1.31:0.26:1；

所述蜗舌4为基于长耳鸮翼型前缘剖面型线的仿生结构。

所述蜗舌4为长耳鸮翼型前缘剖面型线前缘的6.5％。

多翼离心风机的设计方法，多翼离心风机包括蜗壳1、设置在蜗壳1内的叶轮2和蜗舌4以及设置在蜗壳侧面的集流器3，依次对叶轮2、蜗壳1和蜗舌4进行分组改进设计；

叶轮2的改进：所述叶轮2包括轮盘、轮盖和叶片，所述叶片为双圆弧形，首先固定叶片的进口安装角β₁和出口安装角β₂，采用单通道计算模型通过改变两圆弧交接位置R_f和叶片的两圆弧交接位置的安装角为β_f获得不同形状的双圆弧曲线，然后调整叶片的进口安装角β₁和出口安装角β₂，确定进口安装角β₁的变化范围75°～90°，出口安装角β₂的变化范围为160°～180°，不同的两圆弧交接位置R_f和两圆弧交接位置的安装角为β_f对风机效率的影响见图4。最后，采用均匀设计方法在上述设计空间内进行试验设计，基于均匀设计表U31(31³⁰)，选出31个具有代表性的叶轮2样本，并采用CFD数值模拟方法计算出不同形状的叶轮2的效率；

蜗壳1的改进：采用等边基方法对蜗壳1型线重构设计，先根据设计参数确定等边基方，再以等边基方的四角为中心，用四段光滑连接的圆弧片5构成蜗壳1型线，此外，考虑到集流器3与叶轮2的轴向间隙较大，将蜗壳1宽度、集流器3宽度和叶轮2轴向长度的比值设计为1.31:0.26:1，以满足集流器3与叶轮2的轴向匹配，最后将所述叶轮2与蜗壳1进行组合，进行整机CFD计算；

蜗舌4的改进：提取长耳鸮翼型前缘剖面型线并采用Birnbaum-Glauert函数对中心线拟合：

式中：z_c为中弧线坐标；η＝x/c为弦坐标比；x为弦向坐标；z_c(max)为最大弧度坐标；c为翼型弦长；S_n为待定系数，翼型厚度拟合公式为：

式中：z_t为厚度；z_t(max)为最大厚度；A_n为待定系数，式(1)-(2)中的待定系数为：

n＝1时，S_n＝3.9362，A_n＝-29.4861

n＝2时，S_n＝-0.7705，A_n＝66.4565

n＝3时，S_n＝0.8485，A_n＝-59.8060

n＝4时，A_n＝19.0439；

将上述拟合所得的蜗舌4先与蜗壳1匹配后再与叶轮2相结合，进行三维整机CFD计算；

最后将计算结果和实验结果进行对比验证计算模型的可靠性。

计算结果和实验结果的对比：利用ANSYS-CFX商业CFD软件，数值求解三维雷诺平均Navier-Stokes方程组，获得多翼离心风机的气动性能参数和内部流场。考虑到风机内部流动马赫数小于0.3，将其视为不可压缩流动，湍流模型为k-ε模型。在方程离散中，对流项采用高分辨率格式、粘性项采用二阶中心格式、时间导数项采用二阶后向欧拉格式。为降低双吸进去离心风机的流场计算量，仅选取风机的一侧吸气结构进行研究，同时为了方便设定边界条件，对风机的进出口段进行适当延长，最终的计算区域如图2所示。进口给定总压为大气压力和轴向进气条件，出口给定质量流量，壁面满足无滑移边界条件，动静交界面按照多重参考系(Multiple Reference Frame，MRF)方法处理，且进口流域和蜗壳流域采用静止坐标系，叶轮流域采用旋转坐标系来描述。

为提高网格质量，将计算流域首先分为三部分：进口流域、叶轮流域和蜗壳流域。其中，进口流域和蜗壳流域采用ANSYS-ICEM生成非结构混合网格，叶轮流域采用Turbo Grid生成六面体结构网格，对流域近壁区进行适当加密。通过网格无关性验证，当网格总数约为598万，对应三部分流域的网格数分别为43万、385万和170万。

基于上述数值计算模型，对多翼离心风机进行整机数值计算，获得设计流量下的气动性能参数，并与试验数据进行对比，结果如表1所示。可见，风机效率的计算结果与试验数据较为吻合，验证了本文所采用的数值计算方法具有较高的精度。

表1设计流量下试验结果与计算结果对比

效果分析：首先是改进叶轮后的对比分析，结合原始蜗壳和改进后双圆弧形叶片的叶轮，进行整机CFD计算，可得风机效率为73.28％，叶轮效率为89.25％，较原始风机分别提高了1.87％和2.33％。进一步，截取z＝81mm处(以计算区域中的轮盘中心为原点，整个计算区域在z轴正半轴，z＝81mm为叶轮轴向中心处)的叶轮流域和蜗壳流域，观察叶轮改进后风机的内部流场变化情况，如图5-10所示。由图5和6可看出，与原始叶轮相比，改进后叶轮在远离蜗舌流道内的漩涡强度有所减小、流动分离得到缓解，而蜗舌附近流道内的流动分离更加恶化，这说明叶轮与蜗壳间存在较强的耦合作用。从图7-10可看出，风机蜗舌4上部的分离区明显减小，其附近的流场更加均匀，有利于风机气动性能的改善。

其次是改进叶轮2和改进蜗壳1组合后的对比分析，将具有双圆弧形叶片的叶轮2与改进蜗壳1进行组合，进行整机CFD计算，可得风机效率为74.39％，叶轮2效率为89.81％，与上述原始蜗壳和改进后双圆弧形叶片的叶轮2组合起来的风机相比，风机效率和叶轮2效率进一步分别提高了1.11％和0.56％，表明蜗壳1的改进使叶轮2和蜗壳1的性能均得到一定的提高。提取双圆弧形叶片的叶轮2与改进蜗壳1组合下的风机蜗壳1内的绝对速度流线和静压分布，与原始风机以及原始蜗壳和改进后双圆弧形叶片的叶轮2组合起来的风机进行对比，如图11和12所示，可见，改进后蜗壳1内的流动更加均匀，蜗舌4上部流动分离消失，流场分布更加均匀，对应流动损失有所减小，且与原始蜗壳相比，改进后蜗壳1内的静压梯度较均匀，风机效率再次得到提高。

最后是改进叶轮2、改进蜗壳1和改进蜗舌4后的对比分析，为使改进后的仿生蜗舌3与风机的蜗壳1型线匹配良好，设定两个变量，放大倍数scale和旋转角度θ_roate，其变化范围分别是200～800和0°～40°，并根据均匀设计表U₃₁(31³⁰)，通过CFD计算确定出scale和θ_roate的最佳组合。考虑到计算资源的限制，采用二维CFD计算。选取性能最优的蜗壳1样本，如图3所示，将改进蜗舌4与改进的具有双圆弧形叶片的叶轮2相结合，进行三维整机计算，可得风机效率为75.74％，叶轮2效率为90.17％，与仅改进蜗壳1和改进叶轮2而不改进蜗舌的组合相比，风机效率和叶轮2效率分别提高了1.35％和0.36％，与原始风机相比，风机效率和叶轮效率分别提高了4.33％和3.25％。

提取改进蜗舌4与改进的具有双圆弧形叶片的叶轮2相结合风机的流场，如图13和14所示，可见，采用仿生蜗舌4后，蜗壳1内的流动更加均匀，蜗舌4处的分离减小，降低了气体在蜗壳1内的流动损失，使风机效率进一步得到提高，将改进蜗舌4与改进的具有双圆弧形叶片的叶轮2相结合的风机应用到其他工况并与原始风机进行对比，如图15所示，可知，优化后的风机效率整体较原始风机明显提高，气动性能得到改善。

上述描述仅作为本发明可实施的技术方案提出，不作为对其技术方案本身的单一限制条件。