卫星分布式载荷的编队方法与流程
本发明涉及一种卫星自主编队飞行控制方法,特别涉及一种卫星分布式载荷的编队方法。
背景技术:
卫星载荷的编队技术是不同于传统卫星编队的一项新兴技术,是指在同一颗卫星不同位置处布置分布式载荷,并对这些载荷进行编队,使其相对于某一主载荷保持高精度相对位置和相对姿态,以共同完成某些任务。分布式光学成像等大口径光学应用系统对卫星载荷编队技术提出了高精度、高稳定度、超静力学环境等的要求。
传统的卫星编队技术,即对不同的卫星进行编队,一般使用线性化之后的c-w方程来描述两颗卫星之间的相对运动;进行编队控制时,也采用c-w方程来计算控制量。轨控时,采用轨控推力器;姿控时,采用动量轮或姿控推力器两种方式。
文献“申请公布号是cn104142686a的中国发明专利”公开了一种卫星自主编队飞行控制方法。该方法通过轨控使用多次小脉冲喷气、姿控使用动量轮的方式,用于卫星的编队控制,减少了姿态喷气控制对轨道的影响,提高了轨道控制执行精度。该专利中,用喷气推力器提供脉冲力矩,需要消耗大量工质,影响航天器寿命,且容易引起微振动,降低光学部件工作性能;动量轮会存在速度饱和,此后动量轮就不再吸收航天器的多余动量矩,需要进行卸载。此外,空间环境对常规编队卫星影响大,特别是对于低轨卫星,编队受到的环境干扰较复杂,常规编队难度大。总体而言,卫星编队技术的相对位置和相对姿态的控制精度较低,不适用于分布式光学成像这种高精度共相位控制要求。
技术实现要素:
为了克服现有卫星自主编队飞行控制方法控制精度低的不足,本发明提供一种卫星分布式载荷的编队方法。该方法根据任务需求不同,在同一颗卫星的不同位置处布置分布式载荷,载荷编队由一个主载荷和若干个从载荷组成,编队中所有载荷协同工作,完成给定任务。采用分离式stewart驱动平台将卫星本体与载荷相连接,分离式电磁音圈作动器代替可伸缩支腿作为执行机构,采用比例微分(pd)控制律,对分布式载荷进行编队控制。该方法满足了分布式光学成像等大口径光学应用系统提出的高精度、高稳定度、超静力学环境等要求,可完成多种空间任务;同时执行机构不消耗工质,不引起微振动,且无需卸载,有效提高了卫星载荷的控制精度,延长了卫星寿命。
本发明解决其技术问题所采用的技术方案:一种卫星分布式载荷的编队方法,其特点是包括以下步骤:
步骤一、确定卫星上各个部件的位置及其连接方式。
设计分离式stewart驱动平台4。所述分离式stewart驱动平台4以立方体的两个斜界面作为上、下平台,立方体的六条棱作为分离式stewart驱动平台4的六个支腿。采用六个分离式电磁音圈作动器2控制分布式载荷的六自由度运动。卫星本体5分别与分布式主载荷1、第一个分布式从载荷3和第二个分布式从载荷6相连,所述分离式stewart驱动平台4的下平台部分与卫星本体5相连,分离式stewart驱动平台4的上平台部分与分布式主载荷1相连。分离式电磁音圈作动器2与分离式stewart驱动平台4之间采用螺栓连接。
步骤二、确定分布式载荷的相对位置和相对姿态。
在分布式主载荷1、第一个分布式从载荷3和第二个分布式从载荷6上分别安装星敏感器,用于测量载荷相对于惯性坐标系的姿态信息,并利用坐标转换关系,得到需要的相对姿态信息。在分布式主载荷1、第一个分布式从载荷3和第二个分布式从载荷6上安装干涉激光器,用于测量相对位置信息。
步骤三、卫星本体5的姿态动力学建模与控制。
参考坐标系选取卫星本体坐标系oxyz,将卫星本体5当作刚体模型,采用小角度机动假设,即姿态角均为小量,其正弦值为0,余弦值为1,两个小量的乘积忽略,将模型线性化,其模型如下:
其中,ωx,ωy,ωz分别为卫星本体5绕参考坐标系oxyz三轴的转动角速度,ψ,θ,
为使卫星本体5保持稳定,即
加入控制力矩后,卫星本体5的动力学模型为:
其中,
步骤四、分布式载荷的位置和姿态的动力学建模。
将卫星上的分布式主载荷1看作刚体,参考坐标系为分布式主载荷1的本体坐标系op1xp1yp1zp1,假设分布式主载荷1为正方体,则
其中,
以卫星本体坐标系oxyz为参考坐标系,建立分布式主载荷1的位置模型。假设分布式主载荷1只受到分离式stewart驱动平台4通过分离式电磁音圈作动器2施加的力和力矩,并假设载荷为刚体,建立的位置模型如下:
其中,
将第一个分布式从载荷3和第二个分布式从载荷6看作刚体,姿态建模时分别选取第一个分布式从载荷3的本体坐标系op2xp2yp2zp2和第二个分布式从载荷6的本体坐标系op3xp3yp3zp3为参考坐标系;位置建模时选取分布式主载荷1的本体坐标系op1xp1yp1zp1为参考坐标系,建立模型分别为:
其中,
其中,
步骤五、分布式主载荷1相对于卫星本体的位置和姿态的确定。
采用干涉激光器得到分布式主载荷1相对于卫星本体5的位置关系,并将其投影在卫星本体坐标系oxyz中,得到分布式主载荷1相对于卫星本体5的位置为[x1,y1,z1]t。
用星敏感器测得分布式主载荷1相对于惯性坐标系的滚动、俯仰和偏航角为
步骤六、第一个分布式从载荷3和第二个分布式从载荷6相对于分布式主载荷1的位置和姿态的确定。
采用干涉激光器得到第一个分布式从载荷3和第二个分布式从载荷6相对于分布式主载荷1的位置关系,并将其投影在分布式主载荷1的本体坐标系op1xp1yp1zp1中,得到两个从载荷相对于主载荷的位置分别为:[x2,y2,z2]t、[x3,y3,z3]t。
用星敏感器测得分布式主载荷1、第一个分布式从载荷3和第二个分布式从载荷6相对于惯性坐标系的滚动、俯仰和偏航角分别为
步骤七、分布式载荷编队的控制方法。
在完成某一任务时,要求
其中,
其次,要求
其中,
采用比例微分控制方法,分离式电磁音圈作动器2对第二个分布式从载荷6产生的控制力和控制力矩为:
其中,
步骤八、分离式电磁音圈作动器2作为执行机构产生控制力和控制力矩。
分离式电磁音圈作动器2的模型假设为已知,通电电流与产生的输出力的关系如公式(13)所示:
f=bil(13)
其中b,l为分离式电磁音圈作动器的固有属性,当做已知量,i为通过线圈的电流,为可控变量。
进行姿态控制时,设某一作动器的输出力与轴线方向的垂直距离为d,形成沿该载荷轴线方向的力矩,用于控制姿态角的偏差。
步骤九、部分参数的设定。
利用试凑法整定步骤七中所有比例微分参数,先调节比例参数,再调节微分参数,这两个步骤反复进行,直到满足系统要求的性能为止。同时,完成步骤八中分离式电磁音圈作动器2的固有参数b和l的测定,以及分离式电磁音圈作动器2相对于分布式主载荷1、第一个分布式从载荷3和第二个分布式从载荷6的轴线垂直距离d的测量。
本发明的有益效果是:该方法根据任务需求不同,在同一颗卫星的不同位置处布置分布式载荷,载荷编队由一个主载荷和若干个从载荷组成,编队中所有载荷协同工作,完成给定任务。采用分离式stewart驱动平台将卫星本体与载荷相连接,分离式电磁音圈作动器代替可伸缩支腿作为执行机构,采用比例微分(pd)控制律,对分布式载荷进行编队控制。该方法满足了分布式光学成像等大口径光学应用系统提出的高精度、高稳定度、超静力学环境等要求,可完成多种空间任务;同时执行机构不消耗工质,不引起微振动,且无需卸载,有效提高了卫星载荷的控制精度,延长了卫星寿命。
下面结合附图和具体实施方式对本发明作详细说明。
附图说明
图1是本发明卫星分布式载荷的编队方法的流程图。
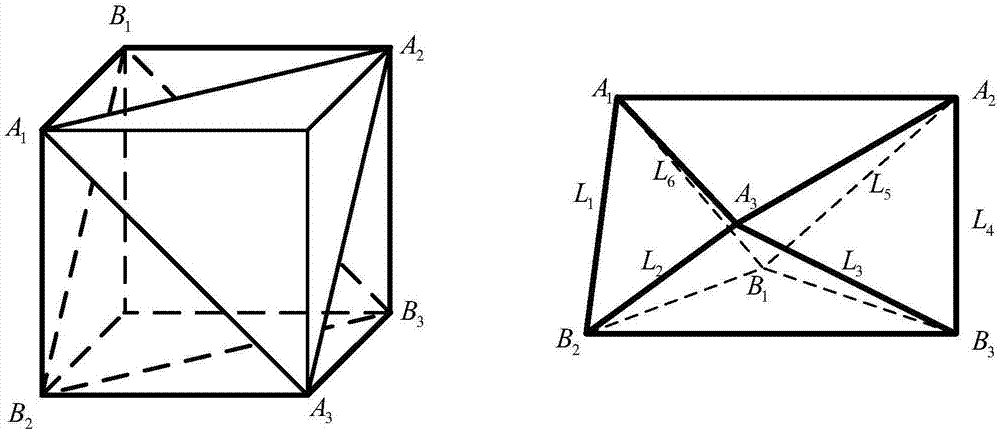
图2是本发明方法所涉及的分离式stewart驱动平台的构型图;
图3是本发明方法所涉及的分离式stewart驱动平台的三维模型图;
图4是本发明方法所涉及的卫星本体、分离式stewart驱动平台、分离式电磁音圈作动器和分布式载荷的连接关系示意图;
图5是本发明方法中分布式载荷编队的控制框图。
图中,1-分布式主载荷,2-分离式电磁音圈作动器,3-第一个分布式从载荷,4-分离式stewart驱动平台,5-卫星本体,6-第二个分布式从载荷。
具体实施方式
参照图1-5。本发明卫星分布式载荷的编队方法具体步骤如下:
步骤一、确定卫星上各个部件的位置及其连接方式。
设计分离式stewart驱动平台4。所述分离式stewart驱动平台4以立方体的两个斜界面作为上、下平台,立方体的六条棱作为分离式stewart驱动平台4的六个支腿。采用六个分离式电磁音圈作动器2代替可伸缩作动器,用于控制分布式载荷的六自由度运动。假设卫星上有三个分布式载荷,分别为分布式主载荷1、第一个分布式从载荷3和第二个分布式从载荷6,确定各个分布式载荷在卫星上的位置,分离式stewart驱动平台4将卫星本体5分别与分布式主载荷1、第一个分布式从载荷3和第二个分布式从载荷6相连,即分离式stewart驱动平台4的下平台部分与卫星本体5相连,上平台部分与分布式主载荷1相连。分离式电磁音圈作动器2与分离式stewart驱动平台4之间采用螺栓连接。
步骤二、确定分布式载荷的相对位置和相对姿态的测量方法。
在每个分布式载荷上安装惯性测量系统如星敏感器,用于测量载荷相对于惯性坐标系的姿态信息,并利用坐标转换关系,得到需要的相对姿态信息。在每个分布式载荷上安装干涉激光器,用于测量相对位置信息。
步骤三、卫星本体5的姿态动力学建模与控制。
对于卫星本体5,不考虑分离式stewart驱动平台4、分布式主载荷1、第一个分布式从载荷3和第二个分布式从载荷6。由于卫星本体5的轨道运动对卫星分布式载荷编队影响不大,故只考虑卫星本体5的姿态运动。参考坐标系选取卫星本体坐标系oxyz,将其当作刚体模型,不考虑环境因素的影响,并采用小角度机动假设,即姿态角均为小量,其正弦值为0,余弦值为1,两个小量的乘积忽略,将模型线性化,其模型如下:
其中,ωx,ωy,ωz分别为卫星本体5绕参考坐标系oxyz三轴的转动角速度,ψ,θ,
由于卫星本体5质量较大,故分离式电磁音圈作动器2产生的输出力对卫星本体5的位置改变可忽略不计。
为使卫星本体5保持稳定,即
加入控制力矩后,卫星本体5的动力学模型为:
其中,
步骤四、分布式载荷的位置和姿态的动力学建模。
将卫星上的分布式主载荷1看作刚体,参考坐标系为分布式主载荷1的本体坐标系op1xp1yp1zp1,假设分布式主载荷1为正方体,则
其中,
以卫星本体坐标系oxyz为参考坐标系,建立分布式主载荷1的位置模型。假设分布式主载荷1只受到分离式stewart驱动平台4通过分离式电磁音圈作动器2施加的力和力矩,并假设载荷为刚体,建立的位置模型如下:
其中,
对于第一个分布式从载荷3和第二个分布式从载荷6,同样的将其看作刚体,姿态建模时分别选取第一个分布式从载荷3的本体坐标系op2xp2yp2zp2和第二个分布式从载荷6的本体坐标系op3xp3yp3zp3为参考坐标系;位置建模时选取分布式主载荷1的本体坐标系op1xp1yp1zp1为参考坐标系,其它假设与建模方法均与分布式主载荷1相同,建立模型分别为:
其中,
其中,
步骤五、分布式主载荷1相对于卫星本体的位置和姿态的确定。
采用干涉激光器可直接得到分布式主载荷1相对于卫星本体5的位置关系,并将其投影在卫星本体坐标系oxyz中,得到分布式主载荷1相对于卫星本体5的位置为[x1,y1,z1]t。
用星敏感器测得分布式主载荷1相对于惯性坐标系的滚动、俯仰和偏航角为
步骤六、第一个分布式从载荷3和第二个分布式从载荷6相对于分布式主载荷1的位置和姿态的确定。
采用干涉激光器可直接得到第一个分布式从载荷3和第二个分布式从载荷6相对于分布式主载荷1的位置关系,并将其投影在分布式主载荷1的本体坐标系op1xp1yp1zp1中,得到两个从载荷相对于主载荷的位置分别为:[x2,y2,z2]t、[x3,y3,z3]t。
用星敏感器测得分布式主载荷1、第一个分布式从载荷3和第二个分布式从载荷6相对于惯性坐标系的滚动、俯仰和偏航角分别为
步骤七、分布式载荷编队的控制方法。
对于卫星分布式载荷的编队技术,在完成某一任务时,首先卫星的分布式主载荷1要按一定的精度相对于卫星本体5的某一位置保持定向,故要求
其中,
其次,第一个分布式从载荷3和第二个分布式从载荷6要相对于分布式主载荷1保持高精度相对位置和相对姿态,即要求
其中,
采用pd控制方法,分离式电磁音圈作动器2对第二个分布式从载荷6产生的控制力和控制力矩为:
其中,
步骤八、分离式电磁音圈作动器2作为执行机构产生控制力和控制力矩。
在上述步骤中,给定各个分布式载荷的参考位置和姿态后,由于空间环境和卫星本体上存在各种干扰,使得各个分布式载荷偏离基准状态,故需要对其进行位置和姿态的补偿。各个分布式载荷的位置和姿态信息可由步骤二中的测量装置得出,然后反馈给控制系统,得出参考值与实际值的差值,按照步骤七所述的pd控制方法进行补偿。
分离式电磁音圈作动器的模型假设为已知,通电电流与产生的输出力的关系如公式(13)所示:
f=bil(13)
其中b,l为分离式电磁音圈作动器的固有属性,可当做已知量,i为通过线圈的电流,为可控变量。
进行姿态控制时,设某一作动器的输出力与轴线方向的垂直距离为d,形成沿该载荷轴线方向的力矩,用于控制姿态角的偏差。
步骤九、上述步骤中各种参数的设定。
此步骤需完成步骤七中所出现的所有比例微分参数的设定,利用试凑法整定这几个参数,先调节比例参数,再调节微分参数,这两个步骤反复进行,直到满足系统要求的性能为止。同时,还需完成步骤八中分离式电磁音圈作动器2的固有参数b和l的测定,以及分离式电磁音圈作动器2相对于分布式主载荷1、第一个分布式从载荷3和第二个分布式从载荷6的轴线垂直距离d的测量。
- 还没有人留言评论。精彩留言会获得点赞!