合金化热浸镀锌钢板的Γ相生成量预测方法以及制造方法与流程

本发明涉及在连续热浸镀生产线制造合金化热浸镀锌钢板中,在镀敷层生成的Γ(capital gamma)相的生成量从制造条件通过基于反应速度论的预测式来预测的方法。还有,还涉及使用了该预测方法的合金化热浸镀锌钢板的制造方法。

背景技术：

合金化热浸镀锌钢板由于以镀敷层为Γ相、δ1相、ζ相等的铁-锌系合金相来构成,因此为锌镀敷钢板的一种的同时,具有挤压成形性(镀敷的模具卡住少)、以及点焊性为良好的特长。但是,合金化过度地进行,则脆的Γ相(Fe₃Zn₁₀)的厚度增大,镀敷钢板加工时(弯曲、弯曲复原、挤压加工、特别是拉深加工时,成形加工等)镀敷层发生以粉状脱落的“粉化现象”,需要挤压模具的清扫·维护的麻烦,在严重的场合,也成为挤压时的加工破裂以及瑕疵的原因。还有,镀敷层的脱落由于也与耐腐蚀性的降低关联,因此在合金化热浸镀锌钢板的品质管理方面,把握、控制这个Γ相的成长的程度为重要,至此在钢铁、汽车各公司开发、实施了各种的方法。作为该方法,大致为以下的那样的方法。

[1]通过设置X线衍射装置等的传感器,镀敷层的合金化度以在线或离线进行测定的方法。

[2]从钢板采取样板,通过镀敷层的分析,测定层中的Fe含有量的方法。

[3]通过对样板实施实际上简易的加工(弯曲、弯曲复原等),把握镀敷层的脱落程度的方法。

以这些的方法测定、把握合金化度,基于该结果,进行合金化处理设备(例如气体燃烧器、诱导加热、或具有并用这些的加热手段的合金化炉)的控制以及通板速度的控制。作为一例,可举专利文献1的技术。

现有技术文献

专利文献

专利文献1:特许第4223238号公报

技术实现要素：

发明所要解决的课题

上述的[1]～[3]的方法是在工业方面确立的技术。但是,[1]是高价的传感器为必要,设备费变膨大,[2]、[3]是为了取样的抽取检查,与全长测定的在线测定相比,存在所谓安心度降低,而且需要人手的问题。

本发明提供如下的方法:合金化热浸镀锌钢板的Γ相生成量通过不要高价的传感器,操作者的劳动负荷低,生产线速度以及钢板温度(合金化炉的温度设定)等的基本的操作数据来以简便而且实用地有用的高精度进行预测的方法。

用于解决课题的手段

为了达成上述目的,本发明中,提供如下的合金化热浸镀锌钢板的Γ相生成量预测方法:在用下述的顺序具有热浸镀锌浴浸渍区、镀敷层的合金化处理中的升温区、镀敷层的合金化处理中的均热区、镀敷层的合金化处理中的冷却区的热浸镀生产线制造合金化热浸镀锌钢板之际,利用通过上述全部区而在镀敷层中生成的Γ(capital gamma)相的总平均厚度Γ_TOTAL(μm)由下述(1)式进行计算来预测的、合金化热浸镀锌钢板的Γ相生成量预测方法。

Γ_TOTAL＝V(T₀)×(t₀-Δt)^1/2…(1)

在此,

V(T₀):镀敷层形成后的热浸镀锌钢板以一定温度T₀(K)进行保持时的Γ相厚度成长速度(μm/sec^1/2),

t₀:从各区通过时间与在各区通过中的每刻的板温的扩散系数求出的、用于以一定温度T₀(K)进行保持而从在T₀(K)的扩散系数算出Γ相的总生成量的换算均热时间(sec),

Δt:起因于镀敷浴浸渍初期的Γ相的生成迟延的迟延时间(sec)。

上述(1)式的换算均热时间t₀中,可以代入从各区的通过时间与在各区通过中的各刻的板温的扩散系数来求出关于Γ相生成量的换算通过时间t₁～t₄的总和t₁+t₂+t₃+t₄。

在此,

t₁:用于以一定温度T₀(K)进行保持而算出热浸镀浴浸渍区通过中的Γ相生成量的换算通过时间(sec),

t₂:用于以一定温度T₀(K)进行保持而算出镀敷层的合金化处理中的升温区通过中的Γ相生成量的换算通过时间(sec),

t₃:用于以一定温度T₀(K)进行保持而算出镀敷层的合金化处理中的均热区通过中的Γ相生成量的换算通过时间(sec),

t₄:用于以一定温度T₀(K)进行保持而算出镀敷层的合金化处理中的冷却区通过中的Γ相生成量的换算通过时间t₄(sec)。

该场合,(1)式成为以下的那样。

Γ_TOTAL＝V(T₀)×(t₁+t₂+t₃+t₄-Δt)^1/2…(1)

以下,如无特别的限定,分别意味着:“浸渍区”为热浸镀浴浸渍区,“升温区”为镀敷层的合金化处理中的升温区,“均热区”为镀敷层的合金化处理中的均热区,“冷却区”为镀敷层的合金化处理中的冷却区。

(1)式的T₀,例如可以设为均热区中的均热温度(钢板的均热保持温度)的值。该场合,上述的换算通过时间t₃,如以合金化炉的均热时间原样使用即可。对每个适用钢种,准备V(T₀)不同的多个(1)式,根据钢种能够分别使用那些的(1)式。代替(1)式,适用付加了以镀敷附着量d(g/m²)的函数g表示的修正项的下述(1)’式为更优选。

Γ_TOTAL＝V(T₀)×(t₀-Δt)^1/2+g(d)…(1)’

还有,本发明中,提供合金化热浸镀锌钢板的制造方法:设定在镀敷层中形成的Γ相生成量的上限规定值,以通过上述的Γ相生成量预测方法来预测的Γ相生成量满足上述上限规定的方式,控制生产线速度、均热区中的均热温度的至少一方。

发明的效果

根据本发明,能够以简便的方法且精度良好地预测合在金化热浸镀锌钢板形成的脆的Γ相的生成量。也不必要利用高价的传感器的计测,由于通过生产线速度以及钢板温度(合金化炉的温度设定)等的基本的操作参数来预测,因此在既存的各种的连续合金化热浸镀生产线的实施也容易。因此,本发明对合金化热浸镀锌钢板的细化的品质管理极其有用。

附图说明

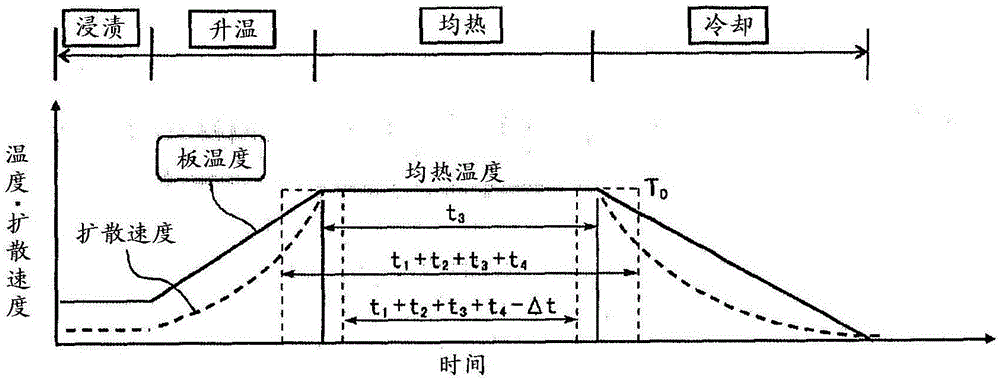
[图1]模拟地例示各区的加热图案的图。

[图2]例示各温度的扩散系数比(vs460℃)的变化的图。

[图3]例示由图2求出的升温中的扩散量S_a与均热中的扩散量S_T之比的温度变化的图。

[图4]例示基于反应速度论的换算均热时间(t₁+t₂+t₃+t₄)的平方根与Γ相厚度的关系的图。

[图5]例示至Γ相成长开始的延迟时间引起的理论-实绩的错位(通过图4的作图而求出的)与均热温度的关系的图。

[图6]例示Γ相成长速度的对数logV与绝对温度的倒数1/T的关系的图。

[图7]对于在镀敷附着量在一定范围的低碳钢,例示(8)式所致的计算值与实测值的关系的图。

[图8]对于包含IF钢的各种的镀敷钢板,例示(8)式所致的计算值与实绩值的关系的图。

[图9]根据钢种,例示通过分别使用(8)式与(9)式而得到的计算值与实绩值的关系的图。

[图10]例示均热温度不足590℃的场合的镀敷附着量与Γ相厚度计算值与实绩值的错位量的关系的图。

[图11]例示均热温度590℃以上的场合的镀敷附着量与Γ相厚度计算值与实绩值的错位量的关系的图。

[图12]例示对使用(10)式～(13)式的钢种的影响以及镀敷附着量的影响进行补正的场合的计算值与实绩值的关系的图。

[图13]例示相当在(8)式的(t₀-Δt)的部分施加补正之前的单纯的均热时间t₃而求出的计算值与实绩值的关系的图。

[图14]例示Γ相厚度计算值(预测值)与粉化评分的关系的图(中·低碳钢,镀敷附着量40g/m²以上不足60g/m²)。

[图15]例示Γ相厚度计算值(预测值)与粉化评分的关系的图(中·低碳钢,镀敷附着量60g/m²以上不足70g/m²)。

[图16]例示Γ相厚度计算值(预测值)与粉化评分的关系的图(中·低碳钢,镀敷附着量70g/m²以上)。

具体实施方式

迄今,在合金化热浸镀锌钢板的制造中,Γ相的生成量的预测方法进行了各种尝试,但利用高价的传感器的测定值如不反馈,预测精度难于充分地提高。根据发明人的研究,作为预测精度的提高难的原因,可以考虑以下的原因。一般的而言,关于合金化热浸镀锌钢板的操作来形成的合金相的预测,在合金化处理炉的到达(目标)温度与该时间(均热时间)进行整理为多,但实际中在镀敷浴进行浸渍之间,合金化反应开始,在合金化处理设备的升温过程、冷却过程中也进行反应。特别是每刻变化的升温·冷却时的原子的扩散量的计算为繁杂,没有考虑了此的数式化。还有,热浸镀锌浴中,添加微量的Al为多,以该影响,在镀敷层/料坯钢板界面中,初期形成阻隔,向锌镀敷层中的Fe原子的扩散开始迟缓,因此预测值与现实存在差。

本发明考虑这些的点,以基于反应速度论的理论式为基础设置加了补正的预测式,由此预测Γ相的生成量。该预测式在通过浸渍区、升温区、均热区、冷却区的各过程而Γ相的总平均厚度成为Γ_TOTAL(μm)的场合中,假设,如果以一定温度T₀(K)保持上述全过程,用于生成相同量的Γ相而必要的均热时间成为如何的程度的、使用所谓换算均热时间t₀(sec)而整理的下述(1)式所示。

Γ_TOTAL＝V(T₀)×(t₀-Δt)^1/2…(1)

在此,V(T₀)是镀敷层形成后的热浸镀锌钢板以一定温度T₀(K)进行保持时的Γ相厚度成长速度(μm/sec^1/2)。t₀是从各区通过时间与在各区通过中的每刻的板温的扩散系数来求出的Γ相的总生成量,用于从以一定温度T₀(K)进行保持的在T₀(K)的扩散系数算出的的换算均热时间(sec)。Δt是起因于镀敷浴浸渍初期的Γ相的生成延迟的迟延时间(sec)。

图1中,模拟地例示各区的加热图案。板温度的变化成为如图1的实线的那样,由于实际的扩散量为exp(1/T)的函数,因此升温中,冷却中的每单位时间的扩散量(扩散速度)成为虚线的那样。

上述(1)式中的一定保持温度T₀(K)可以设定在Zn中Fe原子的扩散进行的(即,Γ相的生成反应进行的)温度域中的任意温度。在以下,将均热区的均热温度(钢板的均热保持温度)作为T₀采用的场合为例进行举例,公开导出(1)式的手法。为了求出换算均热时间t₀,在各温度的Zn中的Fe的给予扩散系数D的式为必要,但方便地通过原子半径为相同程度的过渡金属的数据而可以代用。作为可以代用的元素,可举周期表第4周期第6～11族的Cr、Mn、Co、Ni、Cu(Fe为同第8族元素)。这次是尝试Fe与原子半径近的Ni的活性化能值(Q_Ni＝28919cal/mol)的代用。该场合,扩散系数如以下的那样表示。

D＝D₀·exp(-Q_Ni/(R·T))…(0)

D:扩散系数(m²/sec)

D₀:频度因子

R:气体定数＝1.987(cal/mol/K)

T:绝对温度(K)

Q_Ni:活性化能＝28919(cal/mol)

首先,求出升温区的换算通过时间t₂(sec)与冷却区的换算通过时间t₄(sec)。

图2是在460℃(大概相当于浴温)的扩散系数作为基础(460℃的系数为1)来表示各温度的扩散系数比(vs460℃)的变化的图(以Ni的计算值代用)。在此,在该镀敷生产线的代表的浴温460℃作为基准,但采用根据制造生产线以标准的浴温作为基准的扩散系数比即可。

图3是表示由图2求出升温中的扩散量S_a与均热中的扩散量S_T之比的温度变化。由图3的点的2次曲线近似式,升温·冷却中的扩散量的换算通过温时间t₂(sec)、t₄(sec)成为下述(2a)式、(2b)式的那样。

t₂＝[升温区通过时间]×(0.0000145×[均热温度]²-0.01943×[均热温度]+6.7564)…(2a)

t₄＝[冷却区通过时间]×(0.0000145×[均热温度]²-0.01943×[均热温度]+6.7564)…(2b)

其中,(2a)式、(2b)式中,时间的单位为sec,均热温度的单位为℃(将上述T₀换算成℃)。

其次,对于浸渍区的换算通过时间t₁(sec),通过从图2的曲线在均热温度(将T₀换算成℃的值)的扩散系数与在460℃的扩散系数之比来可以换算,具体是成为下述(3)式的那样。

t₁＝[浸渍时间]/(9.9904×10^-32×[均热温度]^11.656)…(3)

其中,(3)式中,时间的单位为sec,均热温度的单位为℃(将上述T₀换算成℃)。

从上述(2a)式、(2b)式、(3)式,求出通过各区的换算均热时间t₀(sec)＝t₁+t₂+t₃+t₄。t₃中,在此,以均热时间原样代入即可。

其次,尝试Γ相的成长速度式的导入。合金化反应,由于是起因于热引起原子的扩散的反应,基于反应速度论的换算均热时间的平方根与Γ相厚度的关系应该是成为通过原点的直线。因此,使用实验室的合金化热浸镀锌试验装置,将钢板浸渍于热浸镀锌浴之后提起,接着,投入赤外线加热装置通过各种的均热温度与均热时间,制作加热了的试样。调查该试样,进行浸渍时间、升温时间、冷却时间的换算,对换算均热时间的平方根与Γ相厚度的关系进行作图。图4中示出该结果。但是,在作图通过原点的直线的场合,特别是短时间侧的点成为从理论直线大幅错位的结果。

在图4的实际的点中,可知换算均热时间的平方根的值越小的区域,Γ相的成长量越小(错位为大)。这考虑是意指在刚向Γ相生成镀敷浴的浸渍之后不发生。即,刚浴浸渍之后的数秒间,仅Fe-Al系化合物以及δ1相、ζ相成长,这些的相在某程度成长之后,Γ相的成长开始,因此初期的数秒间(5～7秒)成为在Γ相成长反应中无法有助。也就是说,越在长时间侧的点落在直线上是由于横轴为时间的平方根,初期数秒间的错位在作图上变小而不显著的原因。

图5中,例示根据至该Γ相成长开始的延迟时间的理论-实绩的错位与均热温度的关系。这样,通过将各点以近似直线表示,能够算出上述错位(迟延时间)Δt。该Δt是作为上述T₀的函数来表示。在此,由于将T₀设定在均热区的均热温度,因此Δt成为下述(4)式的那样。

Δt＝-0.0069×[均热温度]+9.4993…(4)

其中,(4)式中,Δt的单位为sec,均热温度的单位为℃(将上述T₀换算成℃)。

其次,补正从图4的直线的错位,各点设为落在图4的直线上,图化该图4的各直线(每均热温度)的倾斜(μm/sec^1/2)的对数与均热温度的绝对温度(K)的倒数的关系,成为图6的那样。从图6的直线关系来求出Γ相成长速度的对数logV与绝对温度的倒数1/T的关系,则成为下述(5)。

logV＝-3643×(1/T)+4.0343…(5)

由于阿伦尼乌斯(Arrhenius)的点成为V＝A·exp(-Q/(R·T))的形式,该式的两边设为对数,则成为lnV＝ln(A·exp(-Q/(R·T)))＝lnA-Q/(R·T),将此从自然对数变换成常用对数(系数2.303),分离1/T的项,则成为:

logV＝logA-(1/2.303)×(Q/(R·T))

＝logA-(Q/(2.303×R))×(1/T)…(6)。

在此,以上的(6)式与(5)式成为相同的形式,分别求出:

由logA＝4.0343,A＝10^4.0343＝10822,

由Q/(2.303×R)＝3643,Q＝16671(cal/mol)。

由此,温度T(K)中的Γ相厚度成长速度V(T)(μm/sec^1/2)成为下述(7)式的那样。

V(T)＝10822×exp(-16671/(R·T))…(7)

在由上述的(1)式表示的预测式

Γ_TOTAL＝V(T₀)×(t₀-Δt)^1/2…(1)

的V(T₀)中代入通过(7)式确定的值,在t₀代入前述的t₁+t₂+t₃+t₄的合计值,在Δt中代入通过(4)式确定的值,由此能够预测在钢板通过上述各区的加热图案生成的Γ相的总平均厚度Γ_TOTAL(μm)。

在此的例中,预测式成为下述(8)式。

Γ_TOTAL＝10822×exp(-16671/(1.987×T₀))×(t₀-Δt)^1/2…(8)

以下,以浸渍区的长度(热浸镀锌浴中的钢板的浸渍距离)为7.5m、升温区的长度为8.9m、均热区的长度为7m、冷却区的长度为10m的连续合金化热浸镀锌钢板制造生产线为例,说明本发明。

上述的各式是使用低碳钢来求出活性化能Q的式子。低碳钢以及中碳钢中,以Q＝16671(cal/mol)求出的(8)式是十分的相关。

图7中,对于镀敷附着量在一定范围的低碳钢,例示利用(8)式的计算值(预测值)与实测值的关系。图7中的「换算均热时间补正」是指在(1)式中导入-Δt(后述图8、9、12中相同)。另外,实测值是通过SEM观察镀敷层的截面而测定的Γ相的平均厚度(以下中相同)。从图7可知的那样,通过实验室数据(低碳钢,镀敷附着量为60g/m²)为基础导出的Γ层厚的预测式(8)而求出的计算Γ层厚度(预测值),存在与实际的Γ层厚度高的相关。

图8中,关于不仅是低碳钢,包含IF(Interstitial Free)钢的各种的镀敷附着量的钢板,例示利用(8)式的计算值(预测值)与实绩值的关系。该场合中,在利用(8)式的预测值与实绩值的关系中的偏差变大。

由此接着,尝试利用钢种的补正。低碳钢基材的Ti、Nb添加钢(IF钢)的场合,在粒界中几乎不存在C、N、B等的侵入型的固溶原子。锌镀敷的合金化处理由于是600℃以下的比较的低温的热处理,从料坯钢板的Fe原子的供给对粒界扩散为大。因此,在粒界存在的C、N及B等的侵入型原子少的IF钢,与Fe原子的粒界扩散在低碳钢或中碳钢相比容易,作为该结果,可以考虑向镀敷层的Fe的供给速度变大。为此,利用钢种的补正通过活性化能Q设置为小来进行是妥当的。这次,对于IF钢,从(8)式的预测值与实测值的比较进行倒算,IF钢的活性化能Q比低碳钢小7％左右来预估,适用补正了(8)式的下述(9)式,对于IF钢,也可以得到良好的相关。

Γ_TOTAL＝10822×exp(-15500/(1.987×T₀))×(t₀-Δt)^1/2…(9)

图9中,根据钢种,例示通过分别使用(8)式与(9)式而得到的计算值(预测值)与实绩值的关系。

其次,尝试利用镀敷附着量的补正。即使相同温度、时间的合金化反应,在锌镀敷附着量多的场合,从料坯钢板向锌镀敷层中组入可能的Fe原子的数增大(至表层,Fe原子到达的时间变迟),因此在与料坯钢板的界面附近生成的Γ相的厚度变薄。相反,在锌镀敷附着量少的场合,Fe原子到达至镀敷层的表层部,因此在早期与料坯钢板的界面附近的镀敷层中的Fe浓度增大,Γ相的生成厚度变厚。基于数据进行各种研究,例如将均热温度590℃区分为境界,镀敷附着量的影响变得明确。

图10中,例示均热温度不足590℃的场合的镀敷附着量与Γ相厚度计算值(预测值)与实绩值的错位量的关系。还有图11中,例示均热温度590℃以上的场合的镀敷附着量与Γ相厚度计算值(预测值)与实绩值的错位量的关系。低碳钢以及中碳钢以(8)式、IF钢以(9)式分别求出计算值。因此,求出在(8)式增加修正项的下述(10)式与(12)式,以及在(9)式增加修正项的下述(11)式与(13)式。这些的修正项是相当于上述(1)’式的函数g的项。

〔均热温度不足590℃,在低碳钢、中碳钢中适用的式〕

Γ_TOTAL＝10822×exp(-16671/(1.987×T₀))×(t₀-Δt)^1/2+(47.4-[镀敷附着量])×0.0108…(10)

〔均热温度不足590℃,在IF钢中适用的式〕

Γ_TOTAL＝10822×exp(-15500/(1.987×T₀))×(t₀-Δt)^1/2+(47.4-[镀敷附着量])×0.0108…(11)

〔均热温度590℃以上,在低碳钢、中碳钢中适用的式〕

Γ_TOTAL＝10822×exp(-16671/(1.987×T₀))×(t₀-Δt)^1/2+(51.8-[镀敷附着量])×0.0277…(12)

〔均热温度590℃以上,在IF钢中适用的式〕

Γ_TOTAL＝10822×exp(-15500/(1.987×T₀))×(t₀-Δt)^1/2+(51.8-[镀敷附着量])×0.0277…(13)

这些的式中,镀敷附着量意指每片面的附着量(g/m²)。

图12中,例示将使用(10)式～(13)式的钢种的影响以及镀敷附着量的影响进行补正的计算值(预测值)与实绩值的关系。

为了比较,图13中,例示通过施加补正之前的单纯的均热时间t₃在(8)式中适用的下述(14)式而求出的计算值(预测值)与实绩值的关系。

Γ_TOTAL＝10822×exp(-16671/(1.987×T₀))×t₃^1/2…(14)

对于补正前的图13,可知与图8、图9、图12,越认真地进行补正,预测精度越提高。

实施例

将低碳钢、中碳钢、IF钢用作料坯钢板,以前述的连续合金化热浸镀生产线在各种的条件来制造合金化热浸镀锌钢板。该数据示于表1(a)、表1(b)、表2(a)、表2(b)。表中的“LS”为生产线速度,“TV”为料坯钢板的板厚与生产线速度的积。

关于粉化的调查,首先,进行6t弯曲(180°),接着进行弯曲复原(120°),观察弯曲加工部,根据粉化量,即脱落了的粉状的镀敷层的量的多少,分类评分1～5的5阶段。脱落了的粉状的镀敷层的量越多,成为越低的评分。还有,合金化越进行,Γ层越厚地成长,因此粉化量容易增大,存在评分变低的倾向。

图14、图15、图16中,对于中·低碳钢,示出使用上述(10)式～(13)式而求出的Γ层厚计算值(预测值)与粉化评分的关系。根据镀敷附着量,进行分开而整理成这些3个的图。这样,通过根据镀敷附着量进行分类,得到使用(10)式～(13)式而求出的Γ层厚计算值(预测值)与粉化评分的相关。基于这样的相关,粉化评分的预测也是可能的。另外,中·低碳钢的场合,镀敷附着量成为70g/m²以上,则即使Γ相厚度降低,难得到高的粉化评分(图16)。

在实用方面允许的粉化发生量,由于合金化热浸镀锌的附着量以及合金化热浸镀锌钢板供给的挤压成形的加工度而变得不同。为此,上述的粉化评分即使相同,由于用途而适用可否的判定(是否判定)也不一样。为了参考,在此,根据镀敷附着量,通过一定的基准来判定的粉化评价,在表中例示○(良好)以及×(不良)。

Γ_TOTAL计算值的栏记载的图13、图8、图9、图12的图号,意指在分别对应的图的计算值中使用的数据。

[表1(a)]

表1(a)

[表1(b)]

表1(b)

[表2(a)]

表2(a)

[表2(b)]

表2(b)