一种变截面卧式加工中心立柱结构的利记博彩app

本发明属于机械工程领域，具体涉及一种变截面卧式加工中心立柱结构，作为“框中框”结构卧式加工中心机床的立柱。

背景技术：

近年来，我国机床不断向高精度、高速度的方向发展，对机床提出了更高的要求。机床刚度决定其加工质量，而构件的结构对机床刚度产生较大的影响。因此，对构件结构进行合理设计，能较大改善机床刚度。传统机床结构设计主要采用经验、类比等方法；该类方法缺乏系统的理论指导，在实际设计中，往往出现材料利用率低、设计结构笨重等现象。而且，目前市场上的机床立柱大多为整体铸造形成，传统设计立柱内部有较多的筋板结构，增加了铸造的难度，而且在浇铸时筋板结构易产生砂眼、浇不足等问题，影响立柱的刚度。

技术实现要素：

本发明的目的在于提供一种全新的立柱结构，提高材料的利用率，使其在静动态刚度提高的同时，重量减轻，加工难度降低，节约加工成本。

为了实现上述目的，本发明提供一种变截面卧式加工中心立柱结构，即在外形上做适当的改进，内部结构上，把传统立柱的横纵向十字筋板去除，将立柱截面分段设计为壁厚不断变化的形式。

一种变截面卧式加工中心立柱结构，包括上横梁、下横梁、纵向支撑柱、弧形加强筋，上横梁、下横梁和分别位于左右两侧的纵向支撑柱相互连接组成中空的回字结构，上横梁的截面呈直角梯形，上横梁内部中空，在上横梁内壁设置有弧形加强筋结构，所述纵向支撑柱包括左纵向支撑柱和右纵向支撑柱，左纵向支撑柱和右纵向支撑柱为关于中心立柱结构垂直中线的镜像结构(即左右对称)，在左纵向支撑柱和右纵向支撑柱上分别设置有前侧壁和后侧壁结构，所述前侧壁由第一节前侧壁、第二节前侧壁和第三节前侧壁沿竖直方向由上至下依次连接组成，第一节前侧壁、第二节前侧壁和第三节前侧壁的壁厚由厚至薄依次为第三节前侧壁、第二节前侧壁、第一节前侧壁，第一节前侧壁和第三节前侧壁为均一厚度，第二节前侧壁的壁厚由上至下呈线性均匀增加，所述第一节前侧壁、第二节前侧壁、第三节前侧壁之间的长度比为(10-12):(4-5):(7-9)，所述后侧壁由第一节后侧壁、第二节后侧壁、第三节后侧壁和第四节后侧壁沿竖直方向由上至下依次连接组成，第一节后侧壁、第二节后侧壁、第三节后侧壁和第四节后侧壁的壁厚由厚至薄依次为第四节后侧壁、第三节后侧壁、第二节后侧壁、第一节后侧壁，第一节后侧壁、第三节后侧壁为均一厚度，第二节后侧壁和第四节后侧壁的壁厚由上至下呈线性均匀增加，所述第一节后侧壁、第二节后侧壁、第三节后侧壁、第四节后侧壁之间的长度比为(8-9):(25-26):(5-7):(12-14)；所述下横梁为斜坡结构，斜坡较高的一侧朝向正面，下横梁与上横梁相同皆为内部中空。

进一步的，所述第一节前侧壁、第二节前侧壁、第三节前侧壁之间的长度比优选为(10-11):(4-5):(7-8)。

进一步的，所述第一节后侧壁、第二节后侧壁、第三节后侧壁、第四节后侧壁之间的长度比优选为(8-9):(25-26):(5-6):(12-13)。

进一步的，所述第四节后侧壁与竖直方向的夹角为3°-5°。

进一步的，所述下横梁的斜坡坡度，即斜面与水平面的夹角为20-35度。所述下横梁的斜坡较高的一侧的厚度中线位于立柱下面x向导轨的中线或中线偏下的位置。

本发明的有益效果为：本发明所述的一种变截面卧式加工中心立柱结构是一种全新的立柱结构，采用变优化目标的分步拓扑优化方法，根据拓扑优化结果，在外形上做适当的改进，内部结构上，把传统立柱的横竖向十字筋板去除，将立柱截面分段设计为壁厚不断变化的形式，提高材料的利用率，使其在静动态刚度提高的同时，重量减轻，加工难度降低，节约加工成本。

附图说明

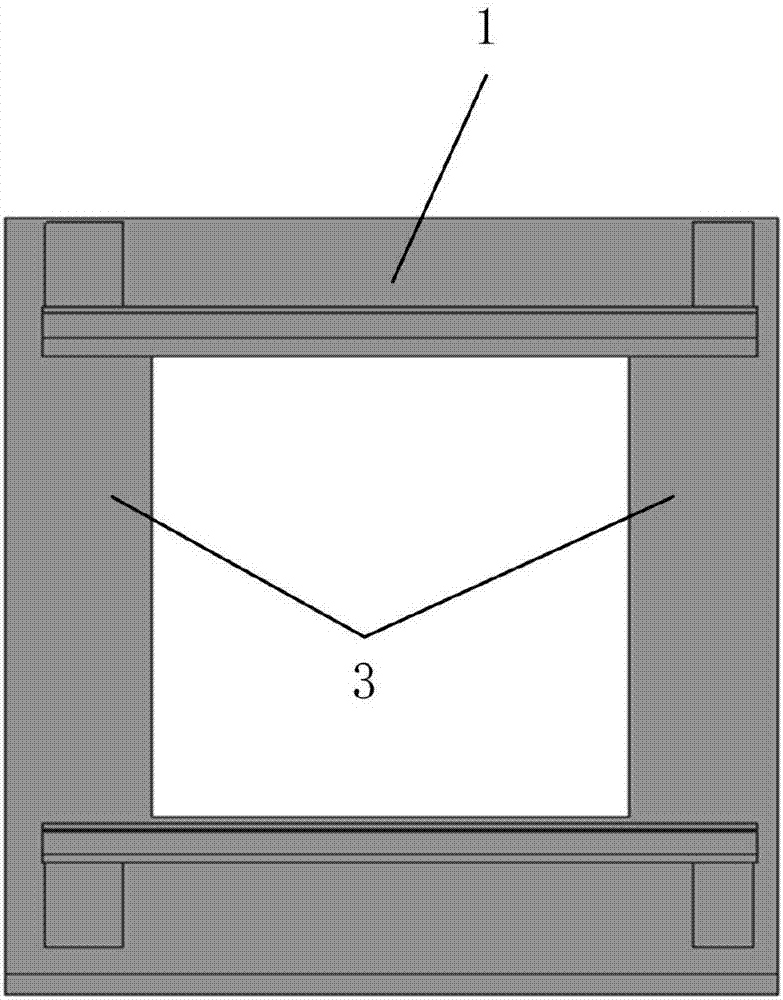
图1是本发明立柱结构的纵向支撑柱截面图。

图2是本发明立柱结构的轴测图(正面)。

图3是本发明立柱结构的轴测图(背面)。

图4是本发明立柱结构的横梁截面图。

图5是gij630卧式加工中心结构示意图。

图6是立柱拓扑优化流程图。

图7是立柱力学模型。

图8是外轮廓拓扑优化结果图1。

图9是外轮廓拓扑优化结果图2。

图10是内部结构拓扑优化结果图1。

图11是内部结构拓扑优化结果图2。

图12是中间工况立柱导轨变形曲线图。

图13是左极限工况立柱导轨变形曲线。

图14是右极限工况立柱导轨变形曲线。

图15是原模型和设计模型一阶振型图。

图16是原模型和设计模型二阶振型图。

图17是原模型和设计模型三阶振型图。

图中：1为上横梁，2为下横梁，3为纵向支撑柱，4为前侧壁，4-1为第一节前侧壁，4-2为第二节前侧壁，4-3为第三节前侧壁，5为后侧壁，5-1为第一节后侧壁，5-2为第二节后侧壁，5-3为第三节后侧壁，5-4为第四节后侧壁，6为弧形加强筋，7为溜板，8为主轴箱，9为立柱，10为床身。

具体实施方式

下面结合附图与具体的实施方式对本发明作进一步详细描述：

如图1所示，该发明立柱为大件产品，整体铸造成型，主要结构包括上横梁1、下横梁2和纵向支撑柱3，上横梁、下横梁和分别位于左右两侧的纵向支撑柱相互连接组成中空的回字结构，上横梁的截面呈直角梯形，在上横梁的一侧为弧形加强筋结构，所述纵向支撑柱包括左纵向支撑柱和右纵向支撑柱，左纵向支撑柱和右纵向支撑柱为关于结构垂直中线的镜像结构，在左纵向支撑柱和右纵向支撑柱分别设置有前侧壁4和后侧壁5结构，所述前侧壁由第一节前侧壁4-1、第二节前侧壁4-2和第三节前侧壁4-3依次连接组成，所述后侧壁由第一节后侧壁5-1、第二节后侧壁5-2、第三节后侧壁5-3和第四节后侧壁5-4依次连接组成，所述下横梁为斜坡结构，斜坡较高的一侧朝向正面。

所述中心立柱结构的高度为2311.50mm；，所述第一节前侧壁、第二节前侧壁、第三节前侧壁的长度依次为1111.50mm、500mm、700mm。

所述第一节后侧壁、第二节后侧壁、第三节后侧壁、第四节后侧壁的长度依次为411.50mm、970mm、250mm、710mm。

基于tosca的卧式加工中心立柱的拓扑优化方法：

1、拓扑优化流程及数学模型

静刚度和动刚度是衡量立柱性能的重要指标，采用线性加权和法将同时提高静动刚度的多目标优化转化为单目标优化。利用有限元软件abaqus和拓扑优化软件tosca对gij630卧式加工中心立柱进行分步拓扑优化：第一步拓扑优化，以多工况柔度最小化和低阶固有频率最大化为优化目标，在满足功能要求和装配条件下，扩大初始优化模型的设计区域，完成立柱外轮廓优化，数学模型如式1；在外轮廓优化的基础上，以多工况变形最小和低阶频率最大为优化目标，约束立柱外轮廓，完成内部结构的优化，数学模型为公式2，提出一种全新的立柱变截面设计方案，使立柱的静动态刚度提高，质量减轻，立柱拓扑优化流程如图6所示。

其中，φ(x)、ω(x)为目标函数；ωi、ωj为加权系数；ci(x)为第i种工况下结构的柔度；u是节点位移矢量；k是结构刚度矩阵；fj是各阶频率；v(x)是优化后模型体积；v0(x)为优化前模型的体积；δ是体积分数，0＜δ＜1；ui(x)为第i种工况下所选节点的变形；ux、uy、uz为节点x、y、z方向的变形矢量。

2立柱载荷分析

gij630卧式加工中心的结构如图5所示，主轴箱嵌入溜板中，由丝杠和滑块导轨副实现y向进给运动；溜板嵌入立柱中，由丝杠牵引，通过起连接作用的导轨滑块副实现x向运动；立柱安装在床身上，起支承溜板和主轴箱的作用。由机床部件的装配关系可知，立柱所受载荷主要来自机床刀具末端的切削力及主轴箱、溜板的重力。

在机床有限元分析中，滑块导轨结合面的载荷分布对机床局部应力影响较大，但对整体应力分布影响较小。在满足整机刚度的前提下，为了方便计算，对结合面的载荷分布做适当的简化处理：(1)受力分析时，忽略滑块导轨副的摩擦，假设移动方向的载荷全部由滚珠丝杠提供；(2)将每个滑块区域的载荷等效为沿着坐标轴方向的集中力，受力点为滑块中点；(3)力单独作用时，每个结合面平均分配该方向载荷；力矩单独作用时，等效为结合面上若干对大小相等、方向相反的力偶；每个结合面最终载荷为各个载荷的叠加[10]。选取主轴箱位于溜板中部时进行分析，以x向滑块与导轨结合面为坐标系x-y平面，四个滑块的对称中心为坐标原点，建立如图7所示的力学模型。

由受力分析，可以求出滑块上的支反力和支反力矩：

按上述力分析简化原则，得到每个滑块上的力为：

式中：fx、fy、fz是滑块上的支反力；mx、my、mz滑块上的支反力矩；fx、fy、fz是刀具末端的切削力；g1为主轴箱重力；g2为溜板重力；fqx表示立柱上丝杠的牵引力；fij表示j滑块处i向的力(i＝x,y,z；j＝1,2,3,4)；a、b、c分别表示刀具末端、主轴箱重心、溜板重心位置；l1、l2分别为滑块x向、y向的跨距。

3、立柱拓扑优化

3.1拓扑优化前处理

根据gij630卧式加工中心立柱的装配关系，提取x、y、z三个方向的最大尺寸，将立柱简化为一个框中框结构的实心质量块，同时保留导轨，轴承座等关键装配部位。

在abaqus中，设置立柱的材料属性为杨氏模量145e9pa，泊松比0.27，密度7.2e3kg/m³。根据机床x向行程，选取溜板处于立柱左极限位置、中间位置和右极限位置三种工况进行静力分析和模态分析，约束立柱底面x、y、z三个方向的移动自由度，采用十节点的四面体单元对立柱进行网格划分，设置导轨、轴承座和底面为冻结区域，进行有限元分析。

3.2外轮廓拓扑优化

将立柱前处理的有限元分析结果.inp文件导入到tosca软件中，采用基于敏度的优化算法，以溜板位于立柱左、右极限位置和中间三个位置的多工况加权静态应变能最小，前三阶固有频率加权最大(权值均为1)为优化目标，以优化后体积与优化前体积的体积比小于等于40％为约束条件，进行拓扑优化，结果如图8、9所示。。

第一步拓扑优化可以得到立柱外轮廓的最优材料分布结果，从中图8、9的模型中提取立柱外轮廓的特征：①上横梁在x方向呈两边窄中间宽的“枣核型”；②上横梁y向为上窄下宽的梯形；③下横梁中间的封闭矩形结构优化为筋板结构。对立柱的外轮廓进行设计，在设计过程中，考虑到立柱上横梁x方向两端在装配中需要安装轴承座，所以将上横梁x方向设计为等宽度，对外轮廓模型进行设计。

3.3内部结构拓扑优化

将外轮廓设计模型作为第二步内部结构拓扑优化的初始模型，在abaqus中对模型进行与外轮廓拓扑优化初始优化模型相同的前处理，冻结区域增加外轮廓表面。为了提高机床的加工质量，应减小导轨的变形，取每种工况下导轨受力点的变形表示导轨的变形。在tosca中，设置目标函数为三种工况下受力点的绝对位移加权最小和前三阶频率加权最大为目标函数，体积约束为小于等于35％，同时添加冻结和对称几何约束，进行第二步拓扑优化，其拓扑优化结果的截面图如图10、11所示。

对拓扑优化结果进行分析，可知与传统的设计相比较，优化模型具有两个特点：①材料集中分布在外轮廓上；②外轮廓材料分布不均匀，壁厚不断变化。根据优化结果，对模型进行内部结构设计。在设计中，外形尺寸保持第一次优化设计结果不变，主要考虑内部壁厚的变化规律，得到最终的优化设计模型。

4优化结果分析

为了验证最终的优化设计模型是否满足静动态性能和轻量化的设计要求，需要对最终的优化设计模型进行有限元分析，并与原模型进行对比。

4.1静刚度校核

立柱静刚度指的是立柱抵抗变形的能力，评价指标为力与该力引起的变形的比值。在载荷相同的情况下，可以用变形来表示刚度的变化，图12、13、14为极限载荷下三种工况立柱导轨的变形曲线，对每种工况下立柱导轨进行xyz三个方向进行校核，选取最大位移代表该种情况下立柱的变形，与原模型进行对比，将变形的减小量转化为静刚度的提高量，结果如表1所示。

表1.立柱变形对比表

从图9中可以看出，新设计模型的导轨变形小于原模型，立柱刚度明显提高；从表1中可以看出，立柱在三个方向的静刚度均有所提高，x向和z向刚度提高较明显，y向刚度提高量较少。由于立柱z向静刚度是相对薄弱的环节，结果显示z向刚度提高幅度较明显，验证了该拓扑优化方法的有效性和新设计结构的合理性。

4.2动刚度校核

对立柱进行分析，不仅要考虑其强度和刚度方面的静态性能，还要分析其弯曲和扭转的动态特性，所以要对立柱进行模态分析。由于低阶模态对机床加工质量的影响较大，所以仅对立柱的前三阶模态进行分析。立柱原模型与优化模型前三阶振型图如图15、16、17所示，频率比较结果如表2所示。

表2.立柱频率对比表

从振型图中可以看出，立柱一阶振型为沿z轴方向的前后俯仰，二阶振型为沿x轴的左右摆动，三阶振型为沿x轴的扭转。

从表2中可以看出，优化后立柱的前三阶频率均得到提高，其中一阶固有频率提高的幅值最大，为40.77％，三阶频率提高也较明显，提高幅度最小的是二阶频率，仅提高了5.15％。经验证，优化后立柱的动态性能符合设计要求。

4.3质量校核

经计算，原立柱模型的质量为4.62t，设计立柱模型的质量为4.14t，减轻了10.39％。因此，立柱新设计模型在静动态性能提高的前提下，实现轻量化设计。

上面结合附图对本发明的基本设计理念进行了描述，但是本发明并不局限于上述的具体实施方式，任何熟悉本专业的技术人员在本发明的启示下，在不脱离本发明宗旨和权利要求所保护的范围内，还可以利用上述内容做出些许改动，但凡根据本发明的技术实质所做的任何改动，仍属于本发明的保护范围之内。