一种汽车转向器摇臂轴齿扇齿廓修形方法与流程

本发明涉及一种汽车转向器摇臂轴齿扇齿廓修形方法，属机械传动技术领域。

背景技术：

汽车驾驶的转向性能取决于转向器摇臂轴齿扇齿条啮合副啮合性能，直线行驶时要求方向盘“重”，稳定；转向时要方向盘“轻”，灵活。尽管可以通过变传动比传动来满足这种汽车驾驶性能，然而，通过摇臂轴齿扇中间齿廓的修形，得到中间齿齿厚更大、齿侧间隙更小，甚至无侧隙啮合的摇臂轴齿扇的转向器更受市场青睐。

齿轮变位的思想由来已久，圆柱齿轮变位应用较普遍，然而这种变位圆柱齿轮，变位量是固定不变的，亦即每个齿的齿厚变化量是均匀相等，相当于渐开线齿廓等距平移，然而这种定变位方法并不适用于汽车转向器摇臂轴非圆齿扇，原因是它不能更好地满足汽车转向性能。一种要求变位能达到齿廓齿厚非均匀变化，即齿扇中间齿廓齿厚大，两边齿廓齿厚小。变变位齿廓修形，即变位量是变化的，可以满足这个要求。

在齿轮传动领域，通过齿轮修形改善传动性能一直是研究的热点问题，较为常见的修形方法是采用磨削工艺手段来实现，但对汽车转向器摇臂轴非圆齿扇采用插削工艺修形还是一个新的研究领域，其中修形中的过切现象存在，必将影响到修形量(或者称为变位量)，如何控制修形量，更好地满足汽车转向器性能需求，是一项重要的研究课题。

《传动技术》(2011，25(4):12-14)刊载了《偏心齿对重合度的影响》论文(作者：张枫念)，提出转向器偏心齿扇齿条副传动，即一种回转中心不在几何中心的非圆齿扇。根据该论文所述技术方案的启示，业内专业人员对这类偏心齿扇进行过研究，并开发了数控加工软件在转向器厂实现了批量生产。该类偏心齿扇的偏心距等于齿扇几何中心与回转中心的偏距，由于该偏心距在齿扇整个转角范围存在，齿扇的中间齿廓齿厚加大，齿侧间隙变小，增强了直线行驶的稳定性，但是，两边齿廓的齿厚若同时加大，则反而降低了转向的灵活性和回正性。

通过变变位系数来减小非圆齿轮副齿侧间隙的设计思想已经出现在非圆齿轮的设计中，例如：论文《变系数移距变位方法及其在非圆齿轮传动中的应用》(谭伟明，《机械工程学报》,2003,39(4):141-144)中提出了在非圆齿扇传动中，使用变系数移距变位方法，用于消除齿轮的根切、增大齿厚和调整传动中心距，能够有效改善齿厚分布和根切现象，其变位系数为事先设定的余弦变化的变位系数函数；论文《变变位齿轮齿侧间隙的试验研究》(陆英，《现代制造工程》，2015(5))中提出了基于节曲线位置变化的变位系数用于消除齿侧间隙。这两种方法都采用线切割加工实验用的齿轮，与实际生产中采用齿条刀具插削加工不同，因此对工业化生产过程的实际实际指导意义非常有限，另一方面，论文中所采用的修形方法相对复杂。

实际插削加工中，采用退刀或进刀的变变位修形存在过切现象，无论变变位运动采用斜坡函数还是余弦函数，过切的存在必将对修形量产生影响，带来修形误差，因此控制修形误差十分重要。针对该问题，论文《非圆齿轮插齿加工中的退刀干涉机理及规避方法研究》(熊镇芹等，《机械工程学报》,2002,38(3):152-155)中，分析了利用三轴数控插齿机插制非圆齿轮产生退刀干涉的原理，提出了一种使插齿刀的回转中心偏离几何中心以规避退刀干涉并实现连续插齿加工的新方法，并以非圆行星齿轮液压马达内齿圈的插制加工为例，给出了这种方法的实施过程和相关算法，通过改变插齿刀的旋转中心，使得插齿刀与工件的连心线与退刀方向一致，从而避免退刀运动对插齿运动的干涉。虽然这种规避退刀干涉的方法和思路很新颖，但致命缺点是刀具回转中心与几何中心不重合，实际上是采用一种偏心齿轮刀具，在插削加工中刀具每转动一圈，每个刀齿受力不均匀，这对刀具的寿命以及加工质量都不利。实际上在修形过程中，存在干涉是不可避免的，关键问题是如何计算出干涉量，并通过参数调整，加以控制。另一方面，该论文提出的技术方案仅是解决用圆盘刀具加工非圆齿轮退刀中的干涉问题，并没有涉及采用齿条刀具加工非圆齿扇(退刀中没有干涉存在)修形中的干涉问题。

通过上述分析可知，偏心本质上就是一种齿扇齿廓的修形，如果将齿扇齿廓修形控制在一定的转角范围，仅对中间齿廓上某一区间段修形，使该段齿厚变大，其余齿厚不变，定能更好地满足所需的转向性能。因此，有必要设计一种变变位齿扇齿廓修形方法，即在插齿加工过程中，齿扇与齿条刀具展成的某一角度范围内，使齿条刀按一种斜坡运动规律后退或前进，从而得到所需的齿扇。

技术实现要素：

本发明目的是针对背景技术提出问题，克服现有技术中汽车转向器摇臂轴齿扇齿廓修形方法的缺陷，提供一种新的汽车转向器摇臂轴齿扇齿廓的变变位修形方法，通过插削加工实现，其变位量采用斜坡函数，该函数是关于齿扇转角的函数，由变位起始、终止角度以及最大变位量三个参数决定，主要是在一定的传动比曲线展成的插削加工过程中，由径向进给轴按斜坡函数运动规律退刀或进刀来实现。通过在变位起始和终止角度范围的变位修形，可以使齿扇的中间一定区间段的齿廓变厚，从而减小汽车转向器齿扇齿条副的啮合间隙，甚至是无侧隙啮合，进一步改善汽车转向性能。该修形方法只需要控制变位的起始、终止角度以及最大变位量三个参数即可实现修形，方法简单，操作方便。由于修形过程中存在过切现象，过切必然减小理论修形量，因此，需要计算理论齿廓与实际齿廓，实际齿廓减去理论齿廓即为实际修形量。分别使用齿廓法线法和包络线法计算理论齿廓和实际齿廓。如果实际修形量不满足理论修形量要求，偏大或者偏小，则调整斜坡函数的变位起始角、终止角以及最大变位量三个参数，重新计算实际修形量，直到满足为止，一旦调整好斜坡函数的三个参数，则固定下来，投入生产中。实践表明这种变变位修形的齿扇齿条副使汽车直线行驶更稳定。从转向器螺母齿条齿扇副的应用发展趋势看，这种直线行驶稳定、转向灵活、平顺的齿条齿扇副更加被市场接受，前景广阔，若能取代传统的转向器，经济效益十分巨大。

本发明的技术方案是：一种汽车转向器摇臂轴齿扇齿廓修形方法，是一种变变位修形方法；其特征在于：所述变变位修形方法依据的计算函数为斜坡函数，所述斜坡函数表达式为：

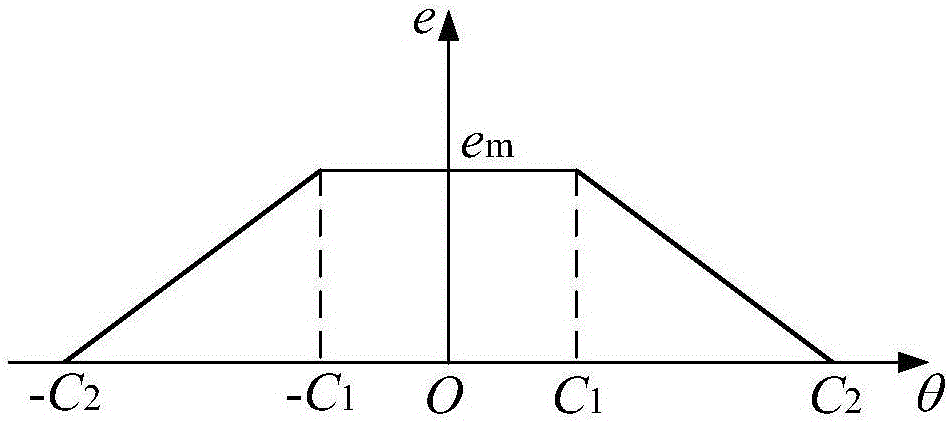
上述公式(1)中：e(θ)是关于齿扇转角θ的函数，其中C₁为变位终止角，C₂变位起始角，e_m为最大变位量，该函数曲线分为三段，在两边[-C₂,-C₁)和(C₁,C₂]区间范围内按线性规律变化，中间[-C₁,C₁]范围保持最大退刀量e_m；

进一步的，针对在修形过程中存在过切现象导致减小理论修形量问题，通过计算理论齿廓与实际齿廓，再将实际齿廓减去理论齿廓，得到实际修形量，并分别使用齿廓法线法和包络线法计算理论齿廓和实际齿廓，当：

实际修形量大于或小于理论修形量时，则调整公式(1)中斜坡函数的变位起始角C₂、变位终止角C₁和最大变位量e_m三个参数，重新计算实际修形量，当实际修形量等于理论修形量时，固化公式(1)中C₂、C₁和e_m三个参数值。

如上所述一种汽车转向器摇臂轴齿扇齿廓修形方法，其特征在于：所述汽车转向器摇臂轴齿扇齿廓的修形过程是在三轴联动的数控插齿机上通过插削加工完成齿廓修形，所述三轴联运数控插齿机的径向进给轴的退刀或进刀运动规律，遵循公式(1)所述斜坡函数运动规律，且：

变位起始角C₂、变位终止角C₁和最大变位量e_m三个参数为已固化值。

本发明的有益效果是：

(1)本发明一种汽车转向器摇臂轴齿扇齿廓修形方法，通过转向器摇臂轴齿扇齿廓的变变位修形，使转向器齿扇齿条副在正中间一定的角度范围的啮合间隙更小，甚至是无侧隙，从而使汽车直线行驶更稳定。为汽车转向器行业提供了一种转向器摇臂轴齿扇齿廓修形新方法。

(2)本发明采用成熟的技术原理，已经实施，并投入使用。

(3)从转向器螺母齿条齿扇副的应用发展趋势看，这种直线行驶稳定，转向灵活、平顺的齿条齿扇副更加被市场接受，前景广阔。

(4)国内商用车产量逐年扩大，每辆车都需要一副，如果能取代传统的转向器，经济效益十分巨大。

附图说明

图1是本发明所采用变变位修形斜坡函数曲线图；

图2是变变位啮合原理图；

图3是变变位齿廓过切示意图；

图4是插削加工齿廓修形原理示意图；

图5是传动比图；

图6是瞬心点轨迹图；

图7是理论齿廓与实际齿廓对比图；

图8是设计变位量、实际变位量与过切量在0～10°时的对比图；

图9a是非圆齿扇加工及齿廓形状在插齿加工与修形过程时的仿真图；

图9b是非圆齿扇加工及齿廓形状在插齿加工与修形后的齿扇齿廓图；

图10a是采用本发明方法加工出的齿扇大端面实物图；

图10b是采用本发明方法加工出的摇臂轴齿扇实物图。

具体实施方式

以下结合附图对本发明实施例作进一步说明，凡在本发明的精神和原则之内所做的任何修改、等同替换或改进等，均应包含在本发明的权利要求范围之内，本技术方案中未详细述及的，均为公知技术。

本发明一种汽车转向器摇臂轴齿扇齿廓修形方法，包括以下步骤：

1)设定修形采用的变位量函数e(θ)为：

参考附图1，上述公式(1)中，e(θ)是关于齿扇转角θ的函数。其中C₁为变位终止角，C₂为变位起始角，e_m为最大变位量。该函数曲线分为三段，在两边[-C₂,-C₁)和(C₁,C₂]区间范围内按线性规律变化，中间[-C₁,C₁]范围保持最大退刀量e_m，形状如斜坡，故称之为斜坡函数。如图1所示，用户只需要设置C₁(变位终止角)、C₂(变位起始角)和e_m(最大变位量)这三个参数，即可完成齿廓修形设置。

2)建立变变位齿扇齿条啮合模型，求解啮合瞬心轨迹

如图2所示，齿扇齿条啮合时，假定齿扇绕定轴坐标系原点转动，齿条做平移运动。以齿扇回转中心为原点，以齿条平移方向为X轴，以齿扇齿条连心线方向为Y轴建立定坐标系[O；x,y]。以齿扇回转中心为原点，以齿扇对称线为Y轴建立齿扇坐标系[O₁；x₁,y₁]。P₀点为无变位运动时齿扇齿条啮合的瞬心点，P₁点为齿扇转动相同角度时，齿扇齿条作变变位啮合时的瞬心点。l₀和l₁分别为无变位运动和变变位运动时，齿条参与啮合的齿廓；K₀、K₁点分别为转动相同角度时，无变位啮合和变变位啮合时的啮合点。

无变位啮合时，根据齿轮啮合理论可知，瞬心点P₀在齿扇与齿条的连心线上，即P₀点在定坐标系O的y轴上。瞬心半径r＝|OP₁|可由下述公式计算：

公式(2)中：p为转向器中丝杠螺母副中螺杆的导程

i为转向器的传动比

齿条的平移的速度为V_0x即为P₀点的速度

V_0x＝|r|ω (3)

变变位啮合时，在有变位的角度范围内啮合时，齿条会附加一个沿着中心线方向的退刀或进刀运动，退刀或进刀速度取决于变位量e(θ)，

变变位啮合时，仍需要保证转向器的传动比，所以此时齿条的横向平移的速度V_1x等于V_0x，

V_0x＝V_0x＝|r|ω (5)

那么，变变位啮合时，齿条的运动速度速度方向角α＝arctan(V_0y/V_0x)。对应齿扇的瞬心点P₁处的速度V₁在大小和方向上均应与V₀相同。考虑方向相同，则图中所示的夹角β＝∠P₀OP₁＝α；再考虑到速度大小相等，则：

将公式(3)代入上述公式(6)中，用R表示OP₁，则有：

R＝r/cosα (7)

在定坐标系下瞬心点运动轨迹方程为：

根据上述公式(8)可知，变变位啮合时，瞬心点在定坐标系下的运动轨迹不再是一条与齿扇齿条连心线重合的直线段，而是一条关于退/进刀速度的曲线。将定坐标系下的瞬心点反向旋转齿扇转过的角度，即可求得齿扇坐标系下的瞬心点，瞬心线方程为可表示为：

公式(9)中：θ表示在当前啮合点啮合时齿扇转动的角度

3)变变位齿扇理论齿廓方程求解

因为啮合点为齿廓在该点的公法线与公切线的交点，则啮合点可由该点的公法线和公切线方程联立求解。啮合点处的公切线方程即为参与啮合的刀具齿廓，而刀具齿廓为直线段，则公切线方程为：

y-y₀＝tan(α₁+π/2)(x-x₀) (10)

公式(10)中：点(x₀，y₀)为齿条上参与啮合的齿廓上的一个已知坐标点；

α₁为齿条上参与啮合的齿廓的压力角。

由Willis定理可知公法线过瞬心，而公法线又与公切线垂直，则公法线方程可表示为：

y-P_1y＝tan(α₁)(x-P_1x) (11)

公式(11)中：(P_1x，P_1y)表示P₁点在定坐标系下的坐标。

P_1x＝Rcos(β+π/2)＝rtan(-α)，

P_1y＝Rcos(β+π/2)＝r。

联立两方程求解，即可计算出啮合点在定坐标系下的坐标。啮合点坐标可由下式计算：

公式(12)为啮合点在定坐标系下的轨迹方程。

再使用点旋转公式，

公式(13)中：θ表示在当前啮合点啮合时齿扇转动的角度

将啮合点绕定坐标系反方向转动齿扇转动的角度，即为齿扇坐标系下的啮合点坐标。公式(13)即为齿廓方程，点(x₁，y₁)为齿廓上任意一点。

4)存在过切现象的证明

如图3所示，为了方便分析，齿扇与齿条啮合时，将齿扇固定，而齿条既要移动，也要转动。K₀、K₁分别表示无变位和变变位的理论计算齿廓。点P₀表示无变位(e(θ)≡0)的情况下，齿条转动θ角度时，齿扇与齿条的啮合点；点P₁表示有变位的情况下，齿条转动θ角度时，齿扇与齿条的啮合点；l₀和l₁分别表示在啮合点P₀和P₁的处的刀具刀刃线。按照设计的传动方式，l₀平行于l₁。n₀和n₁分别表示在啮合点P₀和P₁的公法线，它们分别过各自的瞬心。

图3中V₁为啮合点P₁图示情况下的瞬时速度，V_1x、V_1y分别表示P₁点瞬时法向速度和切向速度。用e(θ)表示变位量关于角度的函数，因为啮合点始终在齿条刀刃线上，则V_1x可由e(θ)计算。V_1x可表示为：

公式(14)中：ω表示齿条转动的角速度。

由于在平面啮合中，定轴转动的齿扇齿条齿廓在任一点啮合的相对运动速度相当于该点以相对角速度绕相对速度瞬心转动的速度，而且因为假定齿扇固定，齿条移动和转动，则齿条相对于齿扇的相对较速度为ω，所以P₁点瞬时切向速度可表示为：

V_1y＝|DP|ω (15)

式中：表示瞬心点到啮合点的长度。

啮合点在理论计算齿廓上的法向速度为与刀具齿廓夹角γ可表示为：

γ＝arctan(e′cosα₁/|DP|) (16)

由公式(14)知，只要e(θ)关于θ的一阶导数不为零，γ就不为0，那么V₁的方向就不与刀刃线重合。当e′|_θ＞0(图3所示情况)时，V₁的方向偏向刀具内部，那么存在一个Δθ＞0，使得齿扇转角时，变变位部分的理论计算齿廓处于当前角度的齿条刀具齿廓线的“上方”，刀具已经切除了即将参与啮合的齿扇啮合点；当e′|_θ＜0时，V₁的方向偏向刀具内部，那么存在一个Δθ＞0，使得齿扇转角时，变变位部分的理论计算齿廓处于当前角度的齿条刀具齿廓线的“下方”，刀具切除了已经加工过的齿廓部分。说明e′|_θ≠0就会导致在齿扇的插齿加工过程中产生过切的现象，从而导致理论啮合点不在最后加工出的齿廓上。

5)实际变位量的计算

这里使用包络线法计算实际齿廓方程。

如图3所示，齿扇与齿条啮合时，将齿扇固定在定坐标系下，齿条做平移和旋转的复合运动。齿扇的齿廓就是齿条上参与啮合的齿廓形成的直线簇的包络。当齿扇转动角度为0时，设定坐标系下的点Q₁(x₁,y₁)为齿条参与啮合的齿廓上的一个固定点(例如齿顶的一个顶点)。当齿条绕固定的齿扇转动θ时，点Q₁移动到点Q₁′。点Q₁′(x₁′,y₁′)在定坐标系下的坐标可表示为：

其中：表示只考虑平移时，点Q₁移动的距离；

齿条上参与啮合的齿廓形成的曲线簇方程可表示为：

F(x,y,θ)＝tan(α)(x-x₁′)-y+y₁′＝0 (18)

式中：α＝π/2+α₁+θ表示齿条转动θ角度后，齿条上参与啮合的齿廓线与定坐标系X轴正向的夹角。

由齿条齿廓直线簇包络出的齿扇坐标方程为：

其中：

将式(17)、(18)和(19)联立求解，得出实际齿廓关于角度θ参数方程：

公式(20)中：I为齿扇齿条传动比(齿扇节点到回转中心的长度)；

k为变位量函数e(θ)对θ的导数；

l为齿条横向移动距离。

用P_n(x_n,y_n)表示无变位的齿廓点，该点的坐标值可由非圆齿轮啮合中的齿廓法线法计算，即公式(13)。用P_p(x_p,y_p)表示在相同工件参数和加工参数下，变变位非圆齿扇实际齿廓点，即公式(20)，该点坐标值由上述的包络线法计算。则实际变位量e_p(θ)可表示为：

6)对比分析与决定

根据公式(21)得到的实际变位量、过切量以及设计的变位量都是关于齿扇转角的函数，将三者进行对比分析。如果实际修形量大于设计修形量，则减小最大变位量e_m；如果实际修形量小于设计修形量，则增大最大变位量e_m。然后根据公式(21)重新计算实际修形量，直到满足要求为止。此时，变位的起始和终止角度也要符合设计要求。这样，修形所采用的斜坡函数的参数就可以固定下来，用于实际加工。

7)变变位修形实现

在三轴联动的数控插齿机上实现。在进行齿扇插齿加工时，通常主运动为刀具的上下冲程运动，进给运动为：径向进给轴Y的前后进给运动，水平移动轴X轴的左右运动，工件旋转轴C轴的旋转运动。其中X、C轴按给定的传动比曲线进行展成运动，如图4所示。本申请提出的变变位修形，即变位系数按斜坡函数规律变化的一种修形方法，通过Y轴的进刀和退刀来完成。因此，齿扇插削加工时，通过X、C、Y三轴联动，即可同时完成修形与展成运动。

进一步的，以下通过一个具体实施例，对本发明作更为详细的说明：

参考附图5所示的传动比图，设定传动比采用分段折线式传动比，变位量函数，斜坡函数如附图1所示。实施例中主要参数如下表1所示：

表1工件加工主要参数表

定坐标系下瞬心点的运动轨迹如图6所示，图6中，瞬心点的位置与转动角度的关系如下表2所示：

表2瞬心点位置与齿扇转动角度关系表

分别计算齿扇理论齿廓和齿扇实际齿廓，得到如图7所示曲线。

由此，设计变位量、实际修形量以及过切量与转动角度关系在0～10°时的对比分析如图8所示。

计算结果表明：齿扇转角θ＝6.1°时，过切量最大，为0.0168mm；θ＝0°时，过切量为0，即实际齿廓在该处与理论齿廓重合。

仿真加工结果如图9a和图9b所示。

实际加工的零件如图10a和图10b所示。经过检验，测试符合用户要求。

通过以上实施例及说明，可以看出，本发明一种汽车转向器摇臂轴齿扇齿廓修形方法，通过转向器摇臂轴齿扇齿廓的变变位修形，使转向器齿扇齿条副在正中间一定的角度范围的啮合间隙更小，甚至是无侧隙，从而使汽车直线行驶更稳定。为汽车转向器行业提供了一种转向器摇臂轴齿扇齿廓修形新方法。

从转向器螺母齿条齿扇副的应用发展趋势看，这种直线行驶稳定，转向灵活、平顺的齿条齿扇副更加被市场接受，前景广阔。由于国内商用车产量逐年扩大，每辆车都需要一副，如果能取代传统的转向器，经济效益十分巨大。

本发明采用成熟的技术原理，已经实施，并投入使用。