用于显微镜LED照明装置的透镜及该透镜的设计方法与流程

本发明涉及一种显微镜LED照明装置，尤其是涉及一种用于显微镜LED照明装置的透镜及该透镜的设计方法。

背景技术：

显微镜是人们洞察微观世界的眼睛。目前在医学、生物学等众多领域中得到了广泛的应用。显微镜的照明方式按其照明光束的形成，可分为“透射式照明”和“落射式照明”两大类，前者适用于透明或半透明的被检物体，后者则适用于非透明的被检物体。

作为21世纪最具有竞争力的新型固体光源，发光二极管(LED)具有体积小、热耗低、寿命长、响应快及显色性好等优点。近年来，随着LED制造成本的减低和应用技术的不断完善，LED在照明领域中被广泛的应用，在显微镜照明上也逐渐取代了传统光源。但是，LED发光特性不同于传统光源，应用在显微镜照明系统时必须进行通过透镜进行光线变换，才能得到视场明亮、照度均匀的圆形光斑，从而提高系统性能。

技术实现要素：

本发明所要解决的技术问题是提供一种体积小、光能利用率高，安装方便，能在显微镜观察区内形成色温均匀的均匀照度分布的用于显微镜LED照明装置的透镜及该透镜的设计方法。

本发明解决上述技术问题所采用的技术方案为：一种用于显微镜LED照明装置的透镜，包括上圆端面、下圆端面和设置在所述的上圆端面和所述的下圆端面之间的环形侧面，所述的上圆端面直径大于所述的下圆端面直径，所述的下圆端面设置有向所述的上圆端面凹陷的空腔，所述的下圆端面与设置在所述的空腔开口处的LED照明装置的发光面平齐，所述的空腔由侧面的柱形第一入射面和顶部的球形第二入射面组成，所述的环形侧面是全反射自由曲面，所述的上圆端面的中间设置有圆形凸起的第一出射面，所述的第一出射面为自由曲面，所述的上圆端面环绕所述的第一出射面的部分构成平面圆环形的第二出射面，从所述的第二入射面入射的光线通过所述的第一出射面出射，从所述的第一入射面入射的光线入射到所述的环形侧面，所述的环形侧面将光线反射到所述的第二出射面出射。

上述的透镜的设计方法，具体步骤如下：

以LED光源为原点O建立坐标系，以LED发光面所在平面为XOY平面，过原点O并与平面XOY垂直的轴为z轴，与z轴交点为o，且平行于平面XOY的平面为照明面，首先对LED光源立体角划分为两部分，中心部分光线和边缘部分光线，并对这两部分光线均匀划分，接着运用能量守恒定律，分别建立这两部分光源立体角与照明面各区域的映射关系，然后利用折反射定律计算得到最后的自由曲面透镜，具体步骤如下：

(1)初始条件的设定和LED光源立体角的划分：

设定目标照明面与LED的距离为H，目标照明区域是一个半径为R的圆形区域，LED光源的总光通量为Φ，中心光强为I₀＝Φ/π，目标照明区域的平均照度为E₀＝I₀/R²，坐标系中为出射光线与z轴正方向的夹角；首先将LED光源立体角划分为两部分：和其中，是0～π/2之间的任意立体角度值，在此基础上，将这两部分立体角分别均匀划分为N等分，则对于LED光源中心部分光线，每一份角度内光源的光通量为：

这里其中和分别是在i份角度和i+1份角度处的立体角度值；

对于LED光源边缘部分光线，每一份角度内光源的光通量为：

这里

因此，LED光源总光通量为：

$\mathrm{\Φ}=\underset{i=1}{\overset{N}{\Σ}}\left({\mathrm{\Φ}}_z\right(i)+{\mathrm{\Φ}}_e(i\left)\right);$

(2)利用能量守恒定律建立光源立体角与照明面环带的映射关系：

先考虑光源边缘部分光线，利用所述的环形侧面将边缘部分光线在照明面上实现圆环照明，圆环内半径为R₀，外半径为R，边缘光线每一份角度内的照度为E_e，由能量守恒定律得：

对于前i份立体角，由能量守恒定律得：

其中，R₀≤r(i)≤R，由以上两式可以得到光源立体角与照明面环带半径的映射关系为：

对于立体角为的光源中心部分光线，首先定义光源立体角的光线在照明面上形成半径为R′₀的均匀圆形光斑，光源立体角的光线在照明面上形成内半径为R′₀，外半径为R的圆环均匀照明，

则由能量守恒定律得：

对于前i份立体角，由能量守恒定律得：

则当时，

由能量守恒定律得：

其中，E₀＝E_e+E_z，

对于前i份立体角，由能量守恒定律得：

则当时，

因此，照明面环带半径r(i)与光源立体角建立了一一对应关系；反复优化调整R₀和R′₀的值，使光源中心部分光线和边缘部分光线在透镜的配光作用下，在照明面上形成均匀的圆形光斑；

(3)计算全反射自由曲面离散点坐标：

由折反射公式求出所述曲面上点的法向量，利用这个法向量求得切平面，通过求切平面与入射光线的交点得到曲面上点的坐标，所述的折反射公式如下：

式中，为入射光线单位向量，为出射光线单位向量，为单位法向量，n为透镜折射率，当发生全反射时，n＝1，

设圆柱空腔半径为d，则立体角为的光线与第二入射面的交点坐标为通过第二入射面后光线的出射角为则

当光线入射到环形侧面时，在该曲面上发生全反射，再在透镜顶部第二出射面上发生折射，若发生折射时的入射角为θ₁(i)，出射角为θ₂(i)，则有

n·sin(θ₁(i))＝sin(θ₂(i))

由几何关系可得：

(h-z)·tan(θ₁(i))+(H-h)·tan(θ₂(i))＝r-x

式中，h为第二出射面的高度，H为光源到照明面的距离，r为照明面对应点所在圆的半径，x,z分别为环形侧面上点的横坐标和纵坐标；

由以上两式求得θ₁(i)，即光线经过全反射后的出射光方向，则在全反射自由曲面上各点的入射光线和出射光线的方向由和θ₁(i)确定；

设透镜宽度为L，则自由曲面初始计算点坐标为此时i＝1，该点的入射光线和出射光线由和θ₁(1)确定，利用折反射定律求出该点的法向量，从而确定该点的切平面，将该切平面与第二条入射光线的相交点确定为第二点，由前一点的切平面与下一点的法向量所在直线相交可得到下一点，通过计算机迭代计算得到透镜环形侧面离散点坐标；

(4)计算第一出射面自由曲面离散点坐标：

中心部分光线经过第一入射面时，由能量守恒定律得到与r(i)的一一对应关系，设透镜的整体高度是s，第一出射面自由曲面的初始点坐标为(0,s)，则利用折反射定律求出初始点的法向量，从而确定该点的切平面，该切平面与第二条的入射光线相交确定为第二点，由前一点的切平面与下一点的法向量所在直线相交可得到下一点，通过计算机迭代计算得到透镜顶部第一出射面自由曲面离散点的坐标；

(5)将计算得到的离散点坐标进行拟合，得到第一出射面自由曲面和环形侧面自由曲面的轮廓曲线，补全第一入射面、第二入射面和第二出射面的轮廓线后得到透镜轮廓曲线，然后将透镜轮廓曲线绕Z轴旋转构成透镜实体。

与现有技术相比，本发明的优点在于光学透镜结构紧凑、体积小巧，适合用于透射式光学显微镜的照明系统。由于透镜外侧采用了全内反射自由曲面，发散角较大的光线也能被利用，大大提高了光学利用率。另外，透镜的内侧是一个空腔，便于LED光源和散热系统的安装。而本发明的设计方法只需要对R₀和R′₀两个参数进行调节，优化参数少，减低了优化难度，缩短设计周期。

附图说明

图1为本发明实施例中LED光源发光立体角的球坐标示意图；

图2为本发明实施例中光学系统配光原理的二维示意图；

图3为本发明实施例中透镜的二维轮廓图；

图4为本发明实施例中透镜的正视三维立体图；

图5为本发明实施例中透镜的俯视三维立体图；

图6为本发明实施例中透镜的仰视三维立体图。

具体实施方式

以下结合附图实施例对本发明作进一步详细描述。

实施例一：依据本发明的方法，以下进行一个具体透镜的设计。以LED光源为原点O建立坐标系，以LED发光面所在平面为XOY平面，过原点O并与平面XOY垂直的轴为z轴，与z轴交点为o，且平行于平面XOY的平面为照明面，首先对LED光源立体角划分为两部分，中心部分光线和边缘部分光线，并对这两部分光线均匀划分，接着运用能量守恒定律，分别建立这两部分光源立体角与照明面各区域的映射关系，然后利用折反射定律计算得到最后的自由曲面透镜，具体步骤如下：

(1)初始条件的设定和LED光源立体角的划分：首先，设定目标照明面与LED的距离为H＝80mm，目标照明区域是一个半径为R＝50mm的圆形区域，LED光源的总光通量为Φ＝100lm，中心光强为I₀＝100/πcd，目标照明区域的平均照度为如图1所示，坐标系中为出射光线101与z轴正方向的夹角，首先将LED光源立体角划分为两部分：和其中在此基础上，将这两部分立体角分别均匀划分为500等分，则对于LED光源中心部分光线，每一份角度内光源的光通量为：

这里其中和分别是在i份角度和i+1份角度处的立体角度值；

对于LED光源边缘部分光线，每一份角度内光源的光通量为：

这里

因此，LED光源总光通量为：

$\mathrm{\Φ}=\underset{i=1}{\overset{N}{\Σ}}\left({\mathrm{\Φ}}_z\right(i)+{\mathrm{\Φ}}_e(i\left)\right);$

(2)利用能量守恒定律建立光源立体角与照明面环带的映射关系：

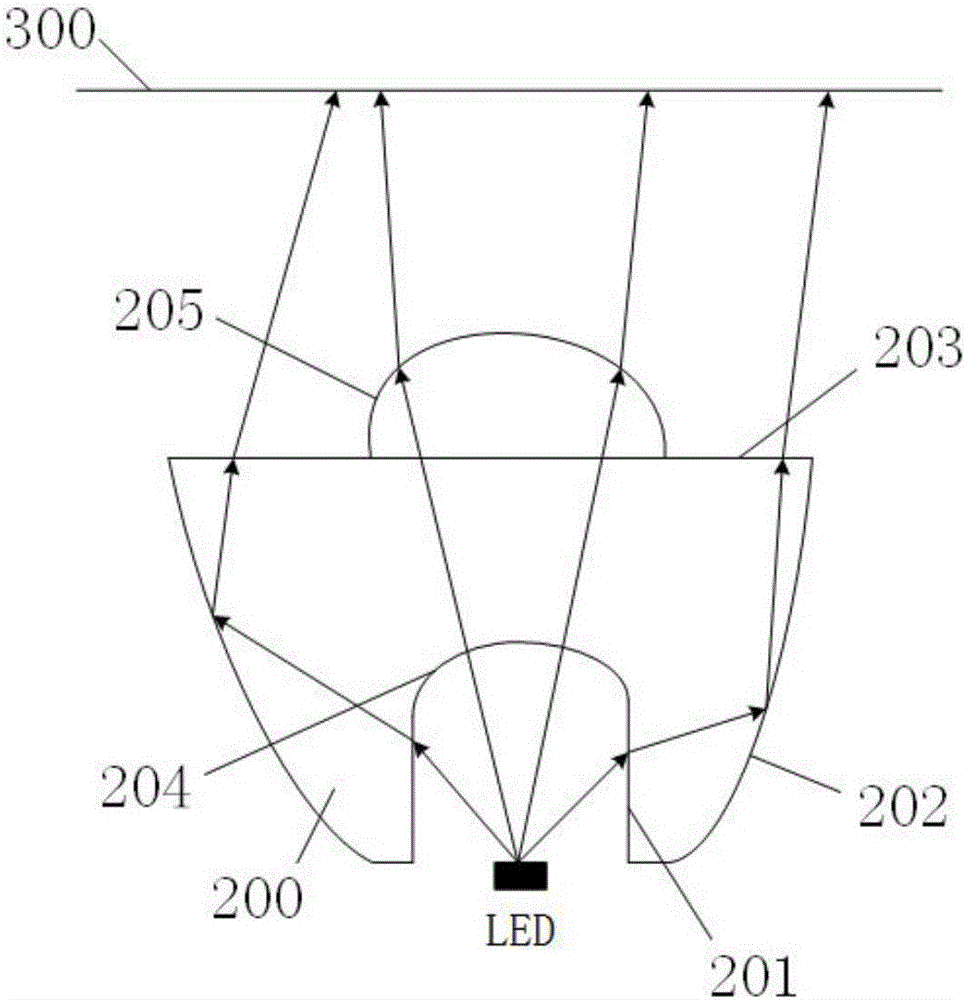
如图2所示，先考虑光源边缘部分光线，利用所述的环形侧面将边缘部分光线在照明面上实现圆环照明，圆环内半径为R₀，外半径为R，入射光线先在透镜内侧柱面第一入射面201折射进入透镜200，再在透镜的环形侧面全反射自由曲面202上发生全发射，接着又在透镜顶部的平面圆环形的第二出射面203折射到照明面300上。边缘光线每一份角度内的照度为E_e，由能量守恒定律得：

对于前i份立体角，由能量守恒定律得：

其中，R₀≤r(i)≤R，由以上两式可以得到光源立体角与照明面环带半径的映射关系为：

对于立体角为的光源中心部分光线，入射光线经过透镜200时，在透镜内侧空腔顶部的半球形第二入射面204入射到透镜200内部，光线方向基本不发生变化，该光线在透镜顶部的圆形凸起的第一出射面205发生折射，出射到照明面300上。由于边缘部分光线在照明面上形成的是圆环照明，所以在对光源中心部分光线的配光时，必须对上述照明面圆环内部的圆形进行光强增强，再在圆环内均匀照明，最终使边缘部分光线和中心部分光线经过透镜后在照明面上形成均匀的圆形光斑，首先定义光源立体角的光线在照明面上形成半径为R′₀的均匀圆形光斑，光源立体角的光线在照明面上形成内半径为R′₀，外半径为R的圆环均匀照明，

则由能量守恒定律得：

对于前i份立体角，由能量守恒定律得：

则当时，

由能量守恒定律得：

其中，E₀＝E_e+E_z，

对于前i份立体角，由能量守恒定律得：

则当时，

因此，照明面环带半径r(i)与光源立体角建立了一一对应关系；反复优化调整R₀和R′₀的值，使光源中心部分光线和边缘部分光线在透镜的配光作用下，在照明面上形成均匀的圆形光斑，经优化调整，R₀＝19.2mm，R′₀＝20mm可以在照明面上形成均匀性较好的圆形光斑；

(3)计算全反射自由曲面离散点坐标：

由折反射公式求出所述曲面上点的法向量，利用这个法向量求得切平面，通过求切平面与入射光线的交点得到曲面上点的坐标，折反射公式如下：

式中，为入射光线单位向量，为出射光线单位向量，为单位法向量，n为透镜折射率，当发生全反射时，n＝1，

设圆柱空腔半径为d＝4mm，则立体角为的光线与第二入射面的交点坐标为通过第二入射面后光线的出射角为则

当光线入射到环形侧面时，在该曲面上发生全反射，再在透镜顶部第二出射面上发生折射，若发生折射时的入射角为θ₁(i)，出射角为θ₂(i)，则有

n·sin(θ₁(i))＝sin(θ₂(i))

由几何关系可得：

(h-z)·tan(θ₁(i))+(H-h)·tan(θ₂(i))＝r-x

式中，h为第二出射面的高度，H为光源到照明面的距离，r为照明面对应点所在圆的半径，x,z分别为环形侧面上点的横坐标和纵坐标；

由以上两式求得θ₁(i)，即光线经过全反射后的出射光方向，则在全反射自由曲面上各点的入射光线和出射光线的方向由和θ₁(i)确定；

设透镜宽度为L＝15mm，则自由曲面初始计算点坐标为此时i＝1，该点的入射光线和出射光线由和θ₁(1)确定，利用折反射定律求出该点的法向量，从而确定该点的切平面，将该切平面与第二条入射光线的相交点确定为第二点，由前一点的切平面与下一点的法向量所在直线相交可得到下一点，通过计算机迭代计算得到透镜环形侧面离散点坐标；

(4)计算第一出射面自由曲面离散点坐标：

中心部分光线经过第一入射面时，由能量守恒定律得到与r(i)的一一对应关系，设透镜的整体高度是16mm，第一出射面自由曲面的初始点坐标为(0,16mm)，则利用折反射定律求出初始点的法向量，从而确定该点的切平面，该切平面与第二条的入射光线相交确定为第二点，由前一点的切平面与下一点的法向量所在直线相交可得到下一点，通过计算机迭代计算得到透镜顶部第一出射面自由曲面离散点的坐标；

(5)将计算得到的离散点坐标导入到机械建模软件，进行拟合，得到如图3所示轮廓线，第一出射面自由曲面和环形侧面自由曲面的轮廓曲线205、202，补全第一入射面、第二入射面和第二出射面的轮廓线后得到透镜轮廓曲线，然后将得到的轮廓曲线绕中心轴旋转360°，即可得到光学透镜实体模型，如图4所示。图5和图6所示分别为透镜三维立体俯视图和仰视图。