一种吸声超结构的利记博彩app

本发明涉及声学共振、吸声技术和声学超结构，尤其涉及一种吸声超结构的单胞结构及其分布。

背景技术：

吸声降噪材料在诸多场合可获得很好的应用，比如汽车、飞机、高铁和轮船等交通运载工具的乘务室降噪、建筑物的降噪、室内空调等家用电器降噪等等。以建筑物的降噪设计为例，一般需要采用密闭的方式隔断建筑物室内空间和室外空间，并且采用合适的吸声材料，吸收从室外传向室内的噪声。但是这种降噪方式会造成密闭的空间，不利于密闭空间和外部的空气流通。此外，如果需要达到较好的降噪效果，选择的吸声材料一般较厚，且价格昂贵。

技术实现要素：

本发明要解决的技术问题是提供一种吸声超结构，其能在非密封的条件下，高效地吸收超结构附近的噪声，隔绝吸声超结构两侧的声波传递。

为了解决上述技术问题，本发明提供一种吸声超结构，包括吸声超结构的单胞结构及其分布。吸声超结构的单胞结构为正六变形；正六变形均分为12个直角三角形；每个直角三角形的内部为声腔，声腔通过细口与外部连通，构成一个Helmholtz共振腔。正六变形空间布置时，采用边对边的布置方式，且留有空气缝隙。此外，空间布置时，中心区域为正六边形空气域；而最外边一层可为完整的正六变形，或者依据所需的几何外形，对正六变形进行裁剪。

作为本发明的吸声超结构的改进：吸声超结构的单胞采用正六变形结构。

作为本发明的吸声超结构的进一步改进：正六变形单胞均分为12个直角三角形。

作为本发明的吸声超结构的进一步改进：正六变形单胞每个直角三角形的内部为Helmholtz共振腔。

作为本发明的吸声超结构的进一步改进：正六变形单胞空间布置时，采用边对边的布置方式，且留有空气缝隙。

作为本发明的吸声超结构的进一步改进：吸声超结构的中心区域为正六边形空气域。

作为本发明的吸声超结构的进一步改进：吸声超结构最外层可为正六变形单胞，或者依据所需的几何外形，对正六变形单胞进行裁剪。

本发明与背景技术相比，具有益的效果是：

该吸声超结构可采用刚度较大的材料(如钢铁和铝合金等)加工而成，生产成本较低。本发明吸声超结构的单极共振可产生负动态体积模量，双极共振可产生负动态质量密度。本发明吸声超结构产生负动态体积模量和负动态质量密度，使声能量聚集在吸声超结构中。本发明通过吸声超结构聚集附近声能量，阻断声波继续向前传播，进而起到降噪的作用。

下面结合附图和具体实施例对本发明作进一步的说明。

附图说明

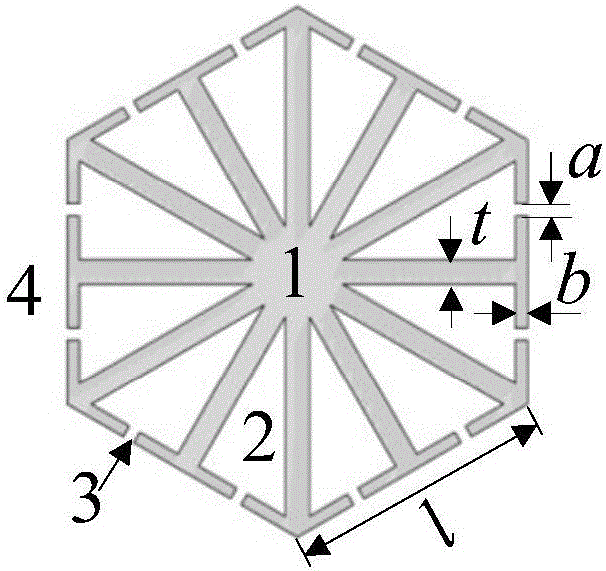
图1是本发明的一种吸声超结构的单胞图；

图2是本发明的一种吸声超结构；

图3是本发明的一种吸声超结构的单极共振和双极共振模态图；

图4是本发明的一种吸声超结构在波导内传递函数及声压场分布图；

具体实施方式

图1给出了一种吸声超结构单胞。单胞为正六边形。1为单胞的材料区域，该材料为刚度较大的材料(如钢铁和铝合金等)。正六边形单胞均分为12直角三角形，每个直角三角形内部为直角三角形声腔2。直角三角形声腔2通过共振短管3与外部声场4联通。直角三角形声腔2与共振短管3构成Helmholtz共振腔。

图2给出了一种吸声超结构。吸声超结构由正六边形单胞排列而成。5为正六边形空气域。正六边形空气域5的外围第一层为6个正六边形单胞，编号分别为6,7,8,9,10和11。每个正六边形单胞的边界与正六边形空气域的边界平行。正六边形空气域5的外围第二层为12个非完整的正六边形单胞，编号为12,13,14,15,16,17,18,19,20,21,22和23。其中，12,13,14,15,16和17为正六变形单胞的一半；18,19,20,21,22和23为正六变形单胞的1/3。正六边形单胞的Helmholtz共振腔通过共振短管3与外部声场4联通。

本发明的吸声超结构工作原理如下：

(1)该吸声超结构单胞的几何参数为a＝1mm,b＝1mm,t＝1mm andl＝14/sin(π/3)mm。

(2)该吸声超结构的几何参数为h＝0.5mm and R＝28.4mm。

(3)将该吸声超结构至于矩形波导中。对吸声超结构进行模态分析，其单极共振和双极共振模态如图3所示。

图3所示的单极共振频率为369Hz。在单极共振频率，压力分布图(图3a)显示声能量聚集在吸声材料的中心区域。相位图(图3b)显示，吸声超结构各方向的相位是近似相等的。因此，单极共振的压力分布和相位图显示声波以同步相位模式(Collective in-Phase Pattern)振动，振动相位与角度无关。图3所示的双极共振频率为758Hz。在双极共振频率，压力分布图(图3c)显示声能量聚集在吸声超结构的左右两侧，且强度近似相等。相位图(图3d)显示，吸声超结构左右两侧的相位成180°互逆。因此，双极共振的压力分布和相位图显示声波沿吸声超结构左右两边、且以180°互逆相位振动。

与传统膜型共振声学超材料(Membrane-Type Metamaterials)和传统Helmholtz共振型声学超材料(Classical Helmholtz-Type Metamaterials)相比，该吸声超结构具有显著地特性。对膜型共振超材料而言，它一阶本征频率的振动形式为双极共振。双极共振频率附近的动态质量密度为负值，这会使得声波传播谱出现Fano型不对称双峰轮廓(Fano-like Asymmetric Dip-Peak Profile)。然而，受膜厚度的限制，模型共振材料很难获得单极共振。传统Helmholtz共振型声学超材料由窄波导和周期型分布的Helmholtz共振腔组成。Helmholtz共振腔短管处流体的运动可产生垂直振动形式。在这种情况，Helmholtz共振腔以半球的形式向周围媒介辐射声波，进而导致单极共振。在单极共振附近，动态体积模量为负值。由于周期性排列的Helmholtz共振腔与波导是解耦的，因此传统Helmholtz共振型声学超材料难以获得双极共振。而本发明设计的吸声超结构同时具有单极共振和双极共振。与Mie共振器类似，声波的同步相位传播会导致吸声超结构的单极共振。此外，由于本发明吸声超结构单胞的直角三角形Helmholtz共振腔的空间排列是对称性破缺的(Symmetry-broken)，因此该吸声超结构可视为对称性破缺型超材料(symmetry-broken formal metamaterial)。对称性破缺的单胞引起的多级散射可导致双极共振。

该吸声超结构的单极共振和双极共振可分别导致负动态体积模量和负动态质量密度。在该吸声超结构中，动态声音传播速度c_m可表示为：

式中，B_m为动态体积模量，ρ_m为动态质量密度。当动态体积模量B_m和动态质量密度ρ_m为负值时，即B_m<0或者ρ_m<0，则等效动态声音传播速度c_m为虚数。

声音传播的波数k_m可表示为：

k_m＝ω/c_m

当等效动态声音传播速度c_m为虚数，则声音传播的波数k_m也为虚数。在这种情况下声波将会聚集在声学超结构之中，而无法继续向前传播。

单极共振和双极共振的标准化频率为

f_r1R/c₀＝0.062

f_r2R/c₀＝0.127

式中f_r1和f_r2分别为单极共振和双极共振的频率；R为吸声超结构的半径；c₀为声音传播速度。

由于标准化的频率都远小于1。因此该吸声超结构为子波长结构，能有效的控制波长较长的声波传播。

(4)吸声超结构的上下边界与波导边界的距离为30mm。沿y方向，吸声超结构的线填充率为62％。吸声超结构的传递函数如图4a所示。分析频带为300Hz-800Hz。在单极共振和双极共振频率之间，声音传递系数较小。这表明吸声超结构有效地阻断了声音的传播。

380Hz和746Hz(分别接近单极共振和双极共振频率)的声压场分布图如图4b和4c所示。声压场分布图显示，吸声超结构右侧波导内的声压分别低于-60dB(380Hz)和-70dH(746Hz)。因此，右侧波导内的声压远低于左侧波导的入射声压0dB。这表明在380Hz和746Hz，声波被完美地阻断了。此外，从图4b可观察到吸声超结构中心空气域的声压幅值大于10dB。这表明，吸声超结构空气域的声压大于周边媒介的声压，声能量聚集在吸声超结构的中心区域。其原因是由于单极共振可导致负动态体积模量；负动态体积模量使得空气在受挤压的情况下出现膨胀现象。我们设计的单胞为刚性边界，则阻止空气的压缩与膨胀。在这种情况，声能量会聚集在单极共振的峰值处，即声能量被吸声超结构中心空气域有效地吸收。

从图4c可观察到吸声超结构外为单胞结构的声压幅值大于10dB。这表明，吸声超结构单胞结构的声压大于周边媒介的声压，声能量聚集在吸声超结构的单胞结构。其原因是由于双极共振可导致负动态质量密度，负动态质量密度使得空气加速的方向与外部激励的方向互逆。我们设计的单胞为刚性边界，则阻止空气逆向运动。在这种情况，声能量会聚集在双极共振的峰值处，即声能量被吸声超结构周边担保结构有效地吸收。

最后，还需要注意的是，以上列举的仅是本发明的一个具体实施例。显然，本发明不限于以上实施例，还可以有许多变形，如圆形、三角形、四变形等。本领域的普通技术人员能从本发明公开的内容直接导出或联想到的所有变形，均应认为是本发明的保护范围。