一种语音识别方法与流程

本发明属于语音识别技术领域，尤其涉及一种语音识别方法。

背景技术：

语音的识别过程主要包括特征提取、特征优化和利用分类器进行识别。在特征提取方面，语音识别系统的性能与识别器所用的特征参数密切相关，常用的特征参数主要有线谱对LSP、相对谱(RASTA)、线性预测倒谱系数LPCC、Mel倒谱MFCC、能量、Fourier倒谱以及相应的动态特征参数等。

小波分析能随信号变化快慢自动调整时间分辨力和频率分辨力。小波系数中少量系数包含信号的绝大部分能量，大部分系数在零附近，对信号能量贡献很小，具有重拖尾现象，因此使用能量/熵特征是不科学的。对于连续小波变换来说，信号小波变换系数模的平方反映了信号在时间-尺度(频率)平面的能量密度分布，对语音多尺度连续小波变换系数采用高斯混合模型(Gaussian Mixture Model,GMM)建模分析，提出新的特征参数GCWT能够有效地区分语音种类。

在特征优化方面，传统的线性降维方法(如主成分分析法(PCA))在把高维数据映射到低维空间时，通常不能保留原高维数据的内在非线性结构和特征。基于流形学习的非线性降维方法局部线性嵌入(Locally linear embedding，LLE)进行降维时，对稀疏采样和噪音污染的数据比较敏感。本发明提出了动态加权局部线性嵌入DWLLE(Dynamic weighted locally linear embedding)方法，对样本点近邻点采用核函数动态加权，弱化稀疏采样对降维造成的影响。

技术实现要素：

解决的技术问题：针对现有的语音识别方法中特征提取方面具有重拖尾现象以及特征优化方面不能保留原高维数据的内在非线性结构和特征的缺点，本发明提供一种语音识别方法，该方法提出的特征参数GCWT优于传统的特征参数MFCC，改进的动态加权局部线性嵌入方法DWLLE的降维效果优于传统的LLE方法。

技术方案：一种语音识别方法包括特征提取、特征优化和利用分类器进行识别三个步骤，本发明主要针对特征提取和特征优化进行研究。在特征提取方面，通过采用多尺度连续小波变换对语音进行时频分析，同时对沿尺度轴方向的小波系数进行高斯混合建模得到统计学参数GCWT，对嗓音进行识别。在特征优化方面，为了降低特征参数的 冗余，对特征参数进行降维处理，针对局部线性嵌入降维算法LLE对稀疏数据的敏感性，提出了改进的动态加权局部线性嵌入降维算法DWLLE。

本发明中的语音识别系统具体设计主要包括：

(1)特征提取阶段，通过采用多尺度连续小波变换对语音进行时频分析，对沿尺度轴方向的小波系数进行高斯混合建模得到特征参数：GCWT＝(π₁,u₁,Σ₁,…,π_M,u_M,Σ_M)

其中，π₁,u₁,Σ₁,…,π_M,u_M,Σ_M分别为M个高斯混合模型的权重、期望、方差。

(2)特征优化阶段，采用动态加权局部线性嵌入方法(DWLLE，Dynamic weighted locally linear embedding)对特征参数GCWT进行降维；

(3)将语音分为训练集与测试集，利用训练集语音的特征参数训练识别模型；

(4)利用训练好的模型对测试集的特征参数进行预测分类。

上述所述的动态加权局部线性嵌入方法DWLLE是对样本点近邻点采用核函数动态加权，弱化稀疏采样对降维造成的影响，主要过程包括：

(1)利用欧氏距离寻找每个样本点的k(k＜n,n为样本点数)个近邻点；

(2)计算样本点和近邻点之间的径向基核函数：

$u_{\mathrm{ij}}=k(x_i,x_j)=\mathrm{\Φ}\left(x_i\right)\·\mathrm{\Φ}\left(x_j\right)=\exp (-\frac{{\left|\right|x_i-x_j\left|\right|}^2}{{\mathrm{\σ}}^2}),$

其中，u_ij是近邻点x_i、x_j的核函数k(x_i,x_j)的函数值，Φ(x_i)、Φ(x_j)分别是样本点x_i、x_j的高维空间映射值，||x_i-x_j||²是样本点x_i、x_j的欧氏距离，σ为函数的宽度参数，控制了函数的径向作用范围。

令θ为加权阈值，当u_ij≥θ时，不对近邻点x_j做任何处理，当u_ij＜θ时，对样本点与近邻点重构之间的误差以u_ij做加权处理，弱化稀疏采样对降维造成的影响；

(3)由样本点的近邻点计算出该样本点的局部重建权值矩阵，使样本点与近邻点以核函数相似度加权的重构误差最小：

$\min \mathrm{\ϵ}\left(W\right)=\underset{i=1}{\overset{n}{\mathrm{\Σ}}}{\left|\underset{j=1}{\overset{k}{\mathrm{\Σ}}}{u}_{\mathrm{ij}}(x_i-w_{\mathrm{ij}}{x}_j)\right|}^2;$

$s.t\underset{j=1}{\overset{n}{\mathrm{\Σ}}}{w}_{\mathrm{ij}}=1$

其中，W是局部重构权值w_ij矩阵，u_ij是动态加权权值，w_ij是样本点x_i、x_j之间的权值，代表着局部信息。

(4)根据局部重建权值矩阵和其近邻点计算出样本集的低维嵌入。

上述所述的特征参数GCWT基于小波变换，充分体现了时域和频域良好的局部化特性。

上述所述的特征参数GCWT是针对小波系数呈现稀疏分布进行改进的特征提取。

有益效果：本发明提供的一种语音识别方法，具有以下优点：

(1)针对小波能量/熵的局限性，通过多尺度连续小波变换对语音进行时频分析，对沿尺度轴方向的小波系数进行高斯混合建模得到统计学参数GCWT，对语音进行识别，提出的特征参数GCWT优于传统的特征参数MFCC。

(2)针对局部线性嵌入降维算法LLE对稀疏数据的敏感性，提出了改进的动态加权局部线性嵌入方法DWLLE，降维效果优于LLE。

附图说明

图1为语音识别系统的主要过程图。

图2为本发明的语音识别系统的设计图。

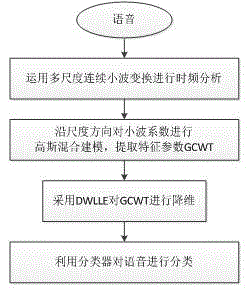
图3为本发明的实施例1的语音识别系统的设计图。

图4为本发明的实施例1的MFCC特征参数提取流程图。

图5为本发明的实施例2的语音识别系统的设计图。

图6为本发明的实施例3的语音识别系统的设计图。

具体实施方式

实施例1

在不进行特征优化的情况下，语音识别包括特征提取和利用分类器进行识别两个步骤。

一、特征提取：

分别对语音提取现有的特征参数MFCC和本发明的特征参数GCWT。

1.特征参数MFCC提取步骤：

(1)将信号S(n)预加重后采用汉明窗进行加窗分帧，得到每帧信号x_n(m)，然后 通过短时傅里叶变换得到其频谱X_n(k)，随后求取频谱的平方，即能量谱P_n(k)。

P_n(k)＝|X_n(k)|²

(2)用M个Mel带通滤波器对P_n(k)进行滤波，由于每一个频带中分量的作用在人耳中是叠加的，因此将每个滤波器频带内的能量进行叠加。

$S_n\left(m\right)=\underset{k=0}{\overset{N-1}{\mathrm{\Σ}}}{P}_n\left(k\right)H_m\left(k\right),1\≤m\≤M$

其中，H_m(k)为Mel滤波器频域形式，S_n(m)是每个滤波器频带输出。

(3)将每个滤波器输出取对数功率谱并进行反离散余弦变换，得到L个MFCC系数。

$C_i^n=\underset{k=1}{\overset{M}{\mathrm{\Σ}}}{\log }_{10}{S}_n\left(k\right)\×\cos [\mathrm{\π}(k-0.5)i/M],1\≤i\≤L$

(4)将得到的MFCC系数作为第n帧的特征参数，反映了语音信号的静态特征，如果加上人耳更为敏感的一阶差分系数，将得到更好的效果。一阶差分的计算公式如下：

$d_i^n=\frac{\underset{j=-L}{\overset{L}{\mathrm{\Σ}}}{c}_{(i+j)}^n\×i}{\sqrt{\underset{j=-L}{\overset{L}{\mathrm{\Σ}}}{j}^2}}$

L一般取2，表示当前帧前后各2帧的线性组合，反映了语音的动态特征。

2.特征参数GCWT提取步骤：

(1)语音时频分析

使用db4小波作为母小波，db4小波的中心频率是0.7143Hz，在16个不同尺度下对语音进行连续小波变换，得到时频域语音的能量谱密度。

(2)高斯混合建模

采用k-menns算法确定中心点进行初始化，并采用EM(Expectation Maximum)算法求解，选取高斯混合模型(M＝4)，对16个小波尺度下的能量谱密度沿尺度方向进行多维建模，并且将建模所得的统计学参数作为特征参数GCWT，GCWT＝(π₁,u₁,Σ₁,…,π_M,u_M,Σ_M)。

二、识别：

使用训练集语音的特征参数训练不同的分类器模型，进而使用训练好模型测试集语音特征参数进行识别。

实施例2

一种语音识别方法包括特征提取、特征优化和利用分类器进行识别三个步骤。

一、特征提取与实施例1中特征参数GCWT提取步骤相同。

二、特征优化：

使用非线性降维方法LLE进行降维处理，包含以下三个步骤：

(1)对于给定的源数据集X＝{x₁,x₂,…,x_n},x_i∈R^D，利用欧氏距离寻找每个样本点的

k(k＜n)个近邻点，其中k＝7；

(2)由样本点的近邻点计算出该样本点的局部重建权值矩阵，使重建误差最小；

(3)根据局部重建权值矩阵和其近邻点计算出样本集的低维嵌入。

LLE在样本均匀采样下使用欧氏距离求取邻域，这对稀疏和噪音污染的数据容易产生扭曲的邻域结构，从而导致短路现象。

三、利用分类器进行识别：

使用经过LLE降维的训练集语音的特征参数训练SVM模型，进而使用训练好模型对经过LLE降维的测试集语音特征参数进行识别。

实施例3

一种语音识别方法包括特征提取、特征优化和利用分类器进行识别三个步骤。

一、特征提取与实施例1特征参数GCWT提取步骤相同。

二、特征优化：

使用非线性降维方法DWLLE对GCWT进行降维处理。降维时，参数设置如下：$k=7,\mathrm{\σ}=\frac{1}{7},\mathrm{\θ}=0.8.$主要过程包括：

(1)利用欧氏距离寻找每个样本点的k(k＜n)个近邻点；

(2)计算样本点和近邻点之间的径向基核函数：

$u_{\mathrm{ij}}=k(x_i,x_j)=\mathrm{\Φ}\left(x_i\right)\·\mathrm{\Φ}\left(x_j\right)=\exp (-\frac{{\left|\right|x_i-x_j\left|\right|}^2}{{\mathrm{\σ}}^2});$

其中，u_ij是近邻点x_i、x_j的核函数k(x_i,x_j)的函数值，Φ(x_i)、Φ(x_j)分别是样本点x_i、x_j的高维空间映射值，||x_i-x_j||²是样本点x_i、x_j的欧氏距离，σ为函数的宽度参数，控制了函数的径向作用范围。

令θ为加权阈值，当u_ij≥θ时，不对近邻点x_j做任何处理，当u_ij＜θ时，对样本点与近邻点重构之间的误差以u_ij做加权处理，弱化稀疏采样对降维造成的影响；

(3)由样本点的近邻点计算出该样本点的局部重建权值矩阵，使样本点与近邻点以核函数相似度加权的重构误差最小：

$\min \mathrm{\ϵ}\left(W\right)=\underset{i=1}{\overset{n}{\mathrm{\Σ}}}{\left|\underset{j=1}{\overset{k}{\mathrm{\Σ}}}{u}_{\mathrm{ij}}(x_i-w_{\mathrm{ij}}{x}_j)\right|}^2;$

$s.t\underset{j=1}{\overset{n}{\mathrm{\Σ}}}{w}_{\mathrm{ij}}=1$

其中，W是局部重构权值w_ij矩阵，u_ij是动态加权权值，w_ij是样本点x_i、x_j之间的权值，代表着局部信息。

(4)根据局部重建权值矩阵和其近邻点计算出样本集的低维嵌入。

三、利用分类器进行识别：

使用经过DWLLE降维的训练集语音的特征参数训练SVM模型，进而使用训练好的模型对经过DWLLE降维的测试集语音特征参数进行识别。

对实施例1中的特征参数MFCC和特征参数GCWT采用十交叉验证方式，实验结果见下表：

从上表可以看出，特征参数GCWT优于传统的特征参数MFCC。

通过实施例2的降维方法LLE对特征参数GCWT降维后识别率分别可以达到95.54％，比实施例1中未经过降维优化的GCWT平均识别率提高了2.7％；实施例3的降维方法DWLLE对特征参数GCWT降维后识别率分别可以达到97.45％，比实施例1中未经过降维优化的GCWT平均识别率提高了4.8％。由此可知，经过降维处理的特征参数比未处理的特征参数提高了系统的识别率和可靠性，并且降维方法DWLLE的降维效果优于降维方法LLE。