基于机身重心位移校正的六足机器人关节角度标定方法与流程
本发明涉及足式移动机器人运动情况的标定方法,属于机器人技术领域,具体地,涉及一种基于机身重心位移校正的六足机器人关节角度标定方法。
背景技术:
相较于轮式移动机器人,足式移动机器人因其具有灵活多变的运动模式,故拥有较强的越障能力,在非结构化环境中具备更好的运动功能鲁棒性。作为足式移动机器人的典型代表,六足移动机器人正逐渐成为足式移动机器人领域研究的热点。
由于六足移动机器人多属于混联机构,运动冗余关节较多,因此其运动控制的准确性及效率难以保证,运动学问题也就成为了六足移动机器人控制理论研究领域的主要热点之一。六足移动机器人的运动精度因其结构特征主要取决于足部各支链的协调与运动轨迹精度,并需要尽量减小足底受力对各关节角度的控制精度影响。因此需要准确的矫正各关节转动角度,从而提高运动轨迹控制精度,降低足底与地面接触冲力。
专利号为201610017524,名为“一种机器人的标定系统及方法”,该发明公开了一种通过计算机采集标定装置的数据以及机器人的关节转角进行运动参数标定的方法。
专利号为201410231904,名为“串联关节式机器人绝对定位误差校准方法及标定系统”,该发明公开了一种通过光学定位仪在上位机中建立被测关节及相邻关节的轴线模型,输出目标转角的网络模型,进行零位误差校准。
但是上述专利存在以下不足:其标定过程需要使用精密光学定位仪或额外位置传感器,增加了标定过程中的额外投入,对于标定过程中的环境也提出了一定的要求。除此以外,需要被标定的机械系统需要增加一定的标定装置以进行零点校准,增加了操作的复杂度以及成本。
技术实现要素:
针对现有技术中的缺陷,本发明的目的是提供一种基于机身重心位移校正的六足机器人关节角度标定方法,以标定一种六足式移动机器人关节零点与旋转角度为目的,建立了关节零点、关节变化量同机器人位姿的映射关系,并结合惯性姿态传感器,本发明的标定方法基于六足机器人原有配置的imu传感器,无需增加额外的仪器或标定装置即可实现零点标定,在六足机器人设计工作范围及设计构型条件下即可满足使用需求。
为实现以上目的,本发明提供一种基于机身重心位移校正的六足机器人关节角度标定方法,即:
驱动六足移动机器人以任意三支撑足支撑地面,选取其中一条支撑足并驱动该支撑足上某一关节发生角度转动,且该支撑足足底滑动,另外两支撑足底与地形不滑动;保持两支撑足固定不动,另外一支撑足转动髋关节;
采用机身配置的imu传感器中的三自由度加速度模块,经二次积分计算机身相对运动轨迹,根据多足移动机器人足-身运动学模型,求解支撑足末端相对机身的坐标,进而校正支撑足各关节角度,从而实现对六足机器人进行全部关节角度标定。
所述六足机器人,其六个结构相同的机械足绕正六边形机身呈旋转对称布置,从机身到足底上的三个关节依次定义为:髋关节、臀关节、膝关节;在六足机器人机身重心处设立机身坐标系,机身坐标系中:xoy平面与机身平面平行、z轴垂直于机身平面;六足髋关节转动轴垂直于机身平面,每个机械足上的臀关节转动轴与膝关节转动轴相互平行且均与机身平面平行。
具体的,所述六足机器人关节角度标定方法,包括如下步骤:
步骤1、初始化imu传感器的三自由度陀螺及三自由度加速度:
步骤2、使六足机器人的某一支撑足转动任意关节角度;
步骤3、读取三自由度加速度数据;
步骤4、若采集到的三自由度加速度均不为0,则记录数据,反之则舍弃该组数据,并重复步骤2及步骤3,直至采集到两组均不为0的三自由度加速度数据;
步骤5、恢复该支撑足关节至步骤1时的初始角度,更换另一条支撑足,并重复步骤2、步骤3和步骤4,直至三条支撑足均完成上述步骤2、步骤3和步骤4操作;
步骤6、得到三条支撑足各两组均不为0的三自由度加速度数据,则转到步骤7求解,若没有得到,继续执行步骤5;
步骤7、根据足底相对机身坐标系的坐标,求解六足机器人三条支撑足中某一支撑足关节角度;
步骤8、重复以上操作,即实现对六足机器人六个支撑足进行关节角度标定。
优选地,步骤1中,利用imu传感器的三自由度陀螺运动感知六足机器人的机身重心在空间中三个方向的加速度;
所述的初始化,通过imu传感器内部的地磁偏角传感器进行校正。
与现有技术相比,本发明具有如下的有益效果:
本发明通过微型惯性传感器获取六足机器人机身姿态角度,结合足式机器人系统运动学与逆运动学模型完成多足运动机器人支撑足各关节角度校正;本发明所述标定方法具有较高的精度和实时性,能快速准确地完成对多足移动机器人关节角度的校正,从而保证机器人多足协调与运动轨迹精度。本发明所述标定方法也可用于检查机器人足关节故障,为机器人运动决策提供依据。
附图说明
通过阅读参照以下附图对非限制性实施例所作的详细描述,本发明的其它特征、目的和优点将会变得更明显:
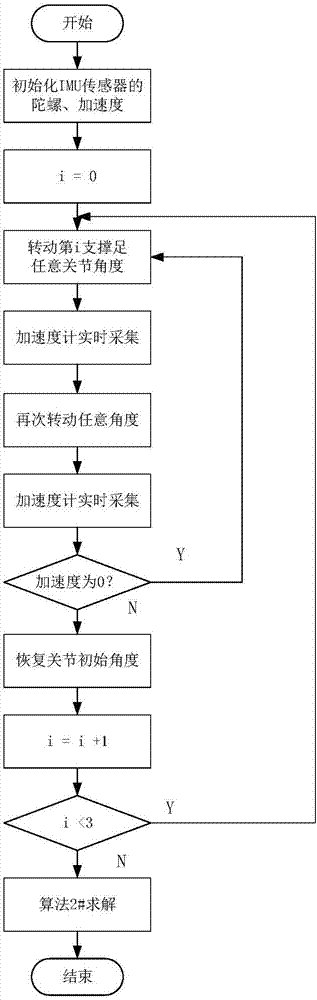
图1为本发明一实施例的方法流程图;
图2为本发明一实施例的集成惯性传感器的六足机器人构型与坐标系示意图;
图3为本发明一实施例的机身关于固定支撑足转动示意简图。
具体实施方式
下面结合具体实施例对本发明进行详细说明。以下实施例将有助于本领域的技术人员进一步理解本发明,但不以任何形式限制本发明。应当指出的是,对本领域的普通技术人员来说,在不脱离本发明构思的前提下,还可以做出若干变形和改进。这些都属于本发明的保护范围。
如图1所示,一种基于机身重心位移校正的六足机器人关节角度标定方法,所述方法针对的六足机器人,其六个结构相同的机械足绕正六边形机身呈旋转对称布置,,以任意三足支撑地面、另外三足抬起并始终保持不接触地面。
所述方法包括如下步骤:
步骤1、初始化imu传感器的三自由度陀螺及三自由度加速度:
如图2所示,从六足机器人的机身到机械足底上的三个关节依次定义为:髋关节、臀关节、膝关节;在六足机器人机身重心处设立机身坐标系,其xoy平面与机身平面平行,z轴垂直于机身平面。六足髋关节转动轴垂直于机身平面,每个机械足上的臀关节转动轴与膝关节转动轴相互平行,且均与机身平面平行;
由于六足机器人支撑至少需要三条足,考虑六足机器人内的三条足机构,并设机械足足底到机身重心位置矢量分别为p1c、p2c、p3c,简化为:pic=(xic,yic,zic)t(i=1,2,3),令αi表示第i个髋关节相对零点的转动角度,βi表示第i个臀关节相对零点的转动角度,γi表示第i个膝关节相对零点的转动角度;髋关节相对于机身重心距离为l1,大腿机构长度为l2,小腿结构长度为l3;(xiα,yiα,ziα)是髋关节在机器人机身坐标系中的坐标。
步骤2、使某一支撑足转动任意关节角度,如图3所示,即使六足机器人重心从o点运动至q1点;
步骤3、读取陀螺三自由度加速度数据;
步骤4、若采集到的三自由度加速度均不为0,则记录数据,反之则舍弃该组数据,重复步骤2、3,直至采集到两组均不为0的三自由度加速度数据,如图3所示六足机器人重心从q1点运动至q2点;
设初始状态时六足机器人机身坐标系c初始时刻与世界坐标系重合,原点坐标为(0,0,0);初始时刻六足机器人的三支撑足足末端在世界坐标系o中的坐标分别为p1o,p2o,p3o,其中:pio=(xio,yio,zio)t;
六足机器人的一个机械足的任意关节发生两次转动,使得六足机器人的机身绕未转动支撑足末端所在直线p1op2o转动;利用加速度计积分,测得六足机器人的重心从坐标原点移动至点q1=(x1,y1,z1)t、q2=(x2,y2,z2)t,可求解直线p1op2o相对于机身坐标系的解析坐标;设直线的单位方向向量为e1=(ex1,ey1,ez1)t,
可由权利要求书中公式(6)求解:
取p1op2o直线上存在一点q01=(x01,y01,z01)t在oq1q2三点确定的平面上,由几何关系可由权利要求书中公式(7)、(8)、(9)解出q01坐标为:
p1op2o方程可由权利要求书中公式(10)表示为:
步骤5、恢复该支撑足关节至步骤1时初始角度,更换另一条支撑足,重复步骤2、3、4;
步骤6、得到三条不同的支撑足各两组均不为0的三自由度加速度数据,通过步骤7求解,反之继续执行步骤5;
与权利要求书中公式(11)、(12)一致,由步骤4中推导方法可解出p2op3o、p3op1o方程分别为:
其中,ex2,ey2,ez2与ex3,ey3,ez3分别为直线p2op3o与p3op1o的单位方向向量坐标,x02,y02,z02与x03,y03,z03分别为直线p2op3o与p3op1o上任意一点q02与q03的坐标,其求解方法如步骤4所述。
步骤7、根据足底相对机身坐标系的坐标,求解六足机器人某一支撑足关节角度;
六足机器人的三个支撑足坐标,为直线p1op2o、p2op3o、p3op1o两两相交的交点坐标,求解三条直线空间方程即可获得足末端相对机身坐标位置;
直线p1op2o、p2op3o、p3op1o理论上两两相交于一点,但鉴于imu传感器噪声及加速度积分误差的存在,使得计算出来的直线位置与实际存在微小偏差,因此可能导致空间内三条直线不相交。因此,通过在三条直线上各搜索两个点分别到另外两条直线距离最短,取相邻两直线上相近的两点的中点作为足末端坐标点。所以,设p1op2o,p2op3o上两点坐标分别由权利要求书中公式(13)、(14)表示为:
x2=ex1m2+x01,y2=ey1m2+y01,z2=ez1m2+z01(13)
x2'=ex2n2+x02,y2'=ey2n2+y02,z2'=ez2n2+z02(14)
其中,为任意常数。
由权利要求书中公式(15):
两直线上最近的两点坐标即满足f最小,由权利要求书中公式(16)、(17)求得此时mi、ni(i=1,2,3):
由权利要求书中公式(18)到(26),得到:
c1=ex1ex3+ey1ey3+ez1ez3(18)
d1=ex1(x01-x03)+ey1(y01-y03)+ez1(z01-z03)(19)
e1=ex3(x01-x03)+ey3(y01-y03)+ez3(z01-z03)(20)
c2=ex1ex2+ey1ey2+ez1ez2(21)
d2=ex1(x01-x02)+ey1(y01-y02)+ez1(z01-z02)(22)
e2=ex2(x01-x02)+ey2(y01-y02)+ez2(z01-z02)(23)
c3=ex3ex2+ey3ey2+ez3ez2(24)
d3=ex3(x03-x02)+ey3(y03-y02)+ez3(z03-z02)(25)
e3=ex2(x03-x02)+ey2(y03-y02)+ez2(z03-z02)(26)
进而求出两连线段中点坐标,求解p1op2o与p1op3o、p2op3o与p1op3o交点坐标得p1o、p2o、p3o的坐标为,由权利要求书中公式(27)、(28)、(29)得:
在求出足末端位置后,代入权利要求书中公式(1)(2)、(3)中求解,可得关节初始值;
即:
其中:
a=(xic-xiα-l1sinαi)2+(yic-yiα-l1cosαi)2(4)
b=(zic-zi0)2(5)
如权利要求书中公式(4)、(5)。需要注意的是,公式(4)(5)有两个解,需要根据六足机器人的运动空间及关节的运动范围限制,选择合适的关节角度。
步骤8、重复以上操作,即可对六足机器人六个支撑足进行关节角度标定。
以上对本发明的具体实施例进行了描述。需要理解的是,本发明并不局限于上述特定实施方式,本领域技术人员可以在权利要求的范围内做出各种变形或修改,这并不影响本发明的实质内容。
- 还没有人留言评论。精彩留言会获得点赞!