一种基于力矩观测和摩擦辨识的机器人接触力检测方法与流程
本发明涉及一种基于力矩观测和摩擦辨识的机器人接触力检测方法,利用机器人动力学方程和广义动量构造力矩观测器来检测机器人末端接触力。
背景技术:
随着制造业从“自动化”、“无人化”向“智能化”、“协作化”的转变,越来越多的生产领域要求工人和机器人共享工作区协同进行工作。在人机共融生产模式下,机器人越来越多的要和周围环境接触,需要对接触力进行严格的控制,因此首先需要检测机器人运行过程中末端执行器受到的接触力。传统的接触力检测主要是基于外部力传感器来实现的,不但增加了成本,还使得机器人控制系统更加复杂。目前比较实用的方法是基于机器人自身传感器的接触力检测方法。这种方法不需要任何外部传感器,大大降低了生产成本,可以直接应用于机器人上。
中国专利CN104050355A公开了一种基于H∞滤波的机械臂外力估计方法,该专利采用模拟低通滤波器对动力学方程进行中信号进行滤波,推导出不显含加速度的动力学模型;将外力看作是状态空间方程的状态变量,基于H∞滤波估计外力;再利用双线性变换的方法设计数字滤波器,从而实现在实际机械臂系统中的应用。该专利提出的方法不能对机器人关节摩擦误差和系统模型误差做出补偿,理论上可行,于实际应用还有待改进。
技术实现要素:
针对现有技术存在的缺陷,本发明的目的是提出一种基于力矩观测和摩擦辨识的机器人接触力检测方法,基于机器人动力学方程和广义动量构造关节接触力矩观测量,利用构造的关节摩擦力矩观测量来辨识机器人关节摩擦参数,将理论运行状态下的观测量视为系统模型误差,在剔除摩擦和系统模型误差的影响后得到了准确的接触力检测值。
为达到上述目的,本发明采用如下技术方案:
一种基于力矩观测和摩擦辨识的机器人接触力检测方法,具体步骤如下:
步骤一:由机器人动力学方程和广义动量构造关节接触力矩观测量,无需采集机器人关节加速度信息,通过构造观测量来非直接检测关节接触力矩,具体为:
机器人动力学方程的一般形式如下:
其中q,是机器人关节的角度矢量,角速度矢量和角加速度矢量,M(q)是机器人的惯性矩阵,是机器人的哥氏力和离心力矢量,G(q)是重力矢量,τj是机器人关节驱动力矩;
当机器人和周围环境发生接触时,接触力的作用会等效到机器人的关节处,产生关节接触力矩,通过观测机器人关节处的接触力矩来检测末端接触力,机器人与周围环境发生接触时的动力学方程为:
其中τe是末端接触力等效到关节处的关节接触力矩;
通过式(2)得出关节接触力矩为:
式(3)中,机器人几何参数和动力学参数通过三维模型得到,关节角度和关节角速度通过机器人关节电机编码器获取,机器人关节电机驱动力矩通过关节驱动电流得到,在忽略机器人模型误差和其他扰动的情况下,机器人关节驱动力矩和关节电机驱动力矩的关系为:
τj=λτm-τf (4)
其中λ为机器人关节的减速比,τf为关节摩擦力矩,关节驱动力矩通过关节电机驱动力矩和关节摩擦力矩求得;为了计算关节接触力矩,需要解决关节角加速度和关节摩擦力矩不能直接获取这个问题,为了解决机器人关节角加速度不能直接获取的问题,引入机器人的广义动量p:
式(5)两边微分得到:
因为M(q)是正定对称矩阵,是斜对称矩阵,所以有:
将式(2)和式(7)代入式(6)得到:
由式(8)看出,动量微分与接触产生的关节接触力矩具有解耦性,并且与关节角加速度无关,基于机器人广义动量来构造关节接触力矩观测量:
其中r为机器人关节接触力矩τe的观测量,K1,K2为系数矩阵;
步骤二:在机器人未与周围环境接触时将关节摩擦力据视为外部扰动构造摩擦力据观测量,采用指数摩擦模型和正余弦函数组合的摩擦模型来辨识摩擦参数,具体为:
机器人未发生接触时考虑摩擦作用的机器人动力学模型为:
基于接触力矩观测的思想构造摩擦力矩观测量为:
其中N为系数矩阵,f为机器人关节摩擦力矩观测量;
将式(11)微分后做拉式变换得到:
由式(12)看出,当N取足够大的值时,认为摩擦力矩观测量在误差允许的范围内能够表示实际的摩擦力矩;
τf=f (13)
机器人关节摩擦模型用指数摩擦模型来表示:
其中τc为库伦摩擦力,τs为静摩擦力,为Stribeck速度,ζ为经验参数,σ为粘性摩擦参数;由于机器人关节存在谐波齿轮传动系统,其摩擦不但包含与速度有关的库伦摩擦与粘性摩擦,还存在与关节角度有关的周期性波动,采用正余弦函数组合的形式来描叙:
τf(q)=K1sin(q)+K2cos(q)+K3sin(2q)+K4cos(2q) (15)
有谐波齿轮传动的关节型机器人的关节摩擦模型用下式表示:
其中Kf等于0表示关节处没有谐波减速器,Kf等于1表示关节处存在谐波传动;
利用式(13)关节摩擦力矩观测量来辨识摩擦参数,将摩擦力矩观测量τf与式(16)计算的摩擦力矩的差值定义为目标函数,对摩擦参数寻优使目标函数最小:
其中n为总的采样点数,这是一个非线性优化问题,采用遗传算法来求解得到关节摩擦参数;
利用辨识的摩擦模型参数计算关节摩擦力矩,考虑摩擦作用后的接触力矩观测量为:
步骤三:将理论运行状态下的观测值视为系统模型误差,通过消除系统模型误差来减小接触力矩观测值误差,根据关节接触力矩和机器人力雅克比矩阵实时计算末端接触力,具体为:
系统模型误差记为rd(t),表示r(t)中的角度、角速度变量都是轨迹规划得到的理论值,考虑系统模型误差后的接触力矩观测量为:
ξ(t)=r(t)-rd(t) (19)
得到机器人关节接触力矩观测量后由式(20)得到末端接触力为:
Fe=(JT(q))-1ξ(t) (20)
其中Fe为末端接触力,JT(q)为机器人雅克比矩阵的转置矩阵。
本发明与现有技术相比较,具有如下突出的实质性特点和显著的优点:
本发明方法不需要在机器人上添加额外的传感器,仅需要采集机器人关节电机电流、关节角度信息即可检测接触力;对于机器人关节复杂的摩擦模型采用观测值辨识摩擦参数,无需直接测量摩擦力矩;将理论运行状态下的观测值视为系统模型误差并剔除其影响,大大提高了检测精度。
附图说明
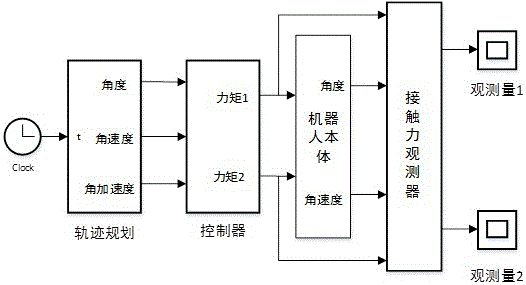
图1是二自由度机器人末端接触力检测示意图。
图2为MTALAB和ADAMS联合仿真系统示意图。
图3是机器人关节摩擦力矩观测值与实际值的对比图。
图4是机器人末端接触力检测值与实际值的对比图。
具体实施方式
以下将结合附图和实施例对本发明的具体实施作进一步说明。
如图1所示为本发明所提出的二自由度机器人末端接触力检测示意图,机器人控制器根据轨迹规划得到的期望轨迹计算出关节驱动力矩驱动机器人运动,关节接触力矩观测器根据反馈回来的机器人关节角度和角速度以及关节驱动力矩来观测关节接触力矩,最后通过雅克比矩阵计算得到末端接触力。
一种基于力矩观测和摩擦辨识的机器人接触力检测方法,具体步骤如下:
步骤一:由机器人动力学方程和广义动量构造关节接触力矩观测量,无需采集机器人关节加速度信息,通过构造观测量来非直接检测关节接触力矩,具体为:
机器人动力学方程的一般形式如下:
其中q,是机器人关节的角度矢量,角速度矢量和角加速度矢量,M(q)是机器人的惯性矩阵,是机器人的哥氏力和离心力矢量,G(q)是重力矢量,τj是机器人关节驱动力矩;
当机器人和周围环境发生接触时,接触力的作用会等效到机器人的关节处,产生关节接触力矩,通过观测机器人关节处的接触力矩来检测末端接触力,机器人与周围环境发生接触时的动力学方程为:
其中τe是末端接触力等效到关节处的关节接触力矩;
通过式(2)得出关节接触力矩为:
式(3)中,机器人几何参数和动力学参数通过三维模型得到,关节角度和关节角速度通过机器人关节电机编码器获取,机器人关节电机驱动力矩通过关节驱动电流得到,在忽略机器人模型误差和其他扰动的情况下,机器人关节驱动力矩和关节电机驱动力矩的关系为:
τj=λτm-τf (4)
其中λ为机器人关节的减速比,τf为关节摩擦力矩,关节驱动力矩通过关节电机驱动力矩和关节摩擦力矩求得;为了计算关节接触力矩,需要解决关节角加速度和关节摩擦力矩不能直接获取这个问题,为了解决机器人关节角加速度不能直接获取的问题,引入机器人的广义动量p:
式(5)两边微分得到:
因为M(q)是正定对称矩阵,是斜对称矩阵,所以有:
将式(2)和式(7)代入式(6)得到:
由式(8)看出,动量微分与接触产生的关节接触力矩具有解耦性,并且与关节角加速度无关,基于机器人广义动量来构造关节接触力矩观测量:
其中r为机器人关节接触力矩τe的观测量,K1,K2为系数矩阵;
步骤二:在机器人未与周围环境接触时将关节摩擦力据视为外部扰动构造摩擦力据观测量,采用指数摩擦模型和正余弦函数组合的摩擦模型来辨识摩擦参数,具体为:
机器人未发生接触时考虑摩擦作用的机器人动力学模型为:
基于接触力矩观测的思想构造摩擦力矩观测量为:
其中N为系数矩阵,f为机器人关节摩擦力矩观测量;
将式(11)微分后做拉式变换得到:
由式(12)看出,当N取足够大的值时,认为摩擦力矩观测量在误差允许的范围内能够表示实际的摩擦力矩;
τf=f (13)
机器人关节摩擦模型用指数摩擦模型来表示:
其中τc为库伦摩擦力,τs为静摩擦力,为Stribeck速度,ζ为经验参数,σ为粘性摩擦参数;由于机器人关节存在谐波齿轮传动系统,其摩擦不但包含与速度有关的库伦摩擦与粘性摩擦,还存在与关节角度有关的周期性波动,采用正余弦函数组合的形式来描叙:
τf(q)=K1sin(q)+K2cos(q)+K3sin(2q)+K4cos(2q) (15)
有谐波齿轮传动的关节型机器人的关节摩擦模型用下式表示:
其中Kf等于0表示关节处没有谐波减速器,Kf等于1表示关节处存在谐波传动;
利用式(13)关节摩擦力矩观测量来辨识摩擦参数,将摩擦力矩观测量τf与式(16)计算的摩擦力矩的差值定义为目标函数,对摩擦参数寻优使目标函数最小:
其中n为总的采样点数,这是一个非线性优化问题,采用遗传算法来求解得到关节摩擦参数;
利用辨识的摩擦模型参数计算关节摩擦力矩,考虑摩擦作用后的接触力矩观测量为:
步骤三:将理论运行状态下的观测值视为系统模型误差,通过消除系统模型误差来减小接触力矩观测值误差,根据关节接触力矩和机器人力雅克比矩阵实时计算末端接触力,具体为:
系统模型误差记为rd(t),表示r(t)中的角度、角速度变量都是轨迹规划得到的理论值,考虑系统模型误差后的接触力矩观测量为:
ξ(t)=r(t)-rd(t) (19)
得到机器人关节接触力矩观测量后由式(20)得到末端接触力为:
Fe=(JT(q))-1ξ(t) (20)
其中Fe为末端接触力,JT(q)为机器人雅克比矩阵的转置矩阵。
如图2所示,为根据构造的接触力矩观测量搭建的MATLAB和ADAMS联合仿真系统,设整个控制系统的控制周期为0.005s。连杆1的长度l1=1m,质量m1=26.5kg,转动惯量Ic1=2.5kgm2,连杆2的长度l2=0.8m,质量m2=21.5kgm2,转动惯量Ic2=1.3kgm2,重力加速度g=9.81m/s2。在MATLAB中利用样条曲线规划机器人运动轨迹,根据计算力矩控制算法控制ADAMS中的机器人运动。
推导式(1)中二自由度机械臂动力学方程的一般形式,在MATLAB中编程计算关节驱动力矩,然后根据式(9)构造关节接触力矩观测量,其中K1=2500,K2=0.04。
图3是机器人关节摩擦力矩观测值与实际值的对比图。在机器人关节处添加摩擦力矩作用,采用本发明中摩擦力矩观测方法观测摩擦力矩,其中实线表示实际添加的摩擦力矩,虚线表示观测的摩擦力矩,从图中看出实线和虚线吻合很好,说明本发明中提出的摩擦力矩观测方法可行。
图4是机器人末端接触力检测值与实际值的对比图。在机器人末端添加接触力作用,如图中实线所示,采用本发明提出的接触力检测方法得到的接触力如图中虚线所示。可以看出,观测的接触力和实际加载的接触力误差较小,说明本发明提出的接触力检测方法可行。
- 还没有人留言评论。精彩留言会获得点赞!