径向小高度加翼大直径钢管桩及其水平承载力计算方法与流程
本发明涉及一种径向小高度加翼大直径钢管桩及其水平承载力计算方法,属于风电基建工程
技术领域:
。
背景技术:
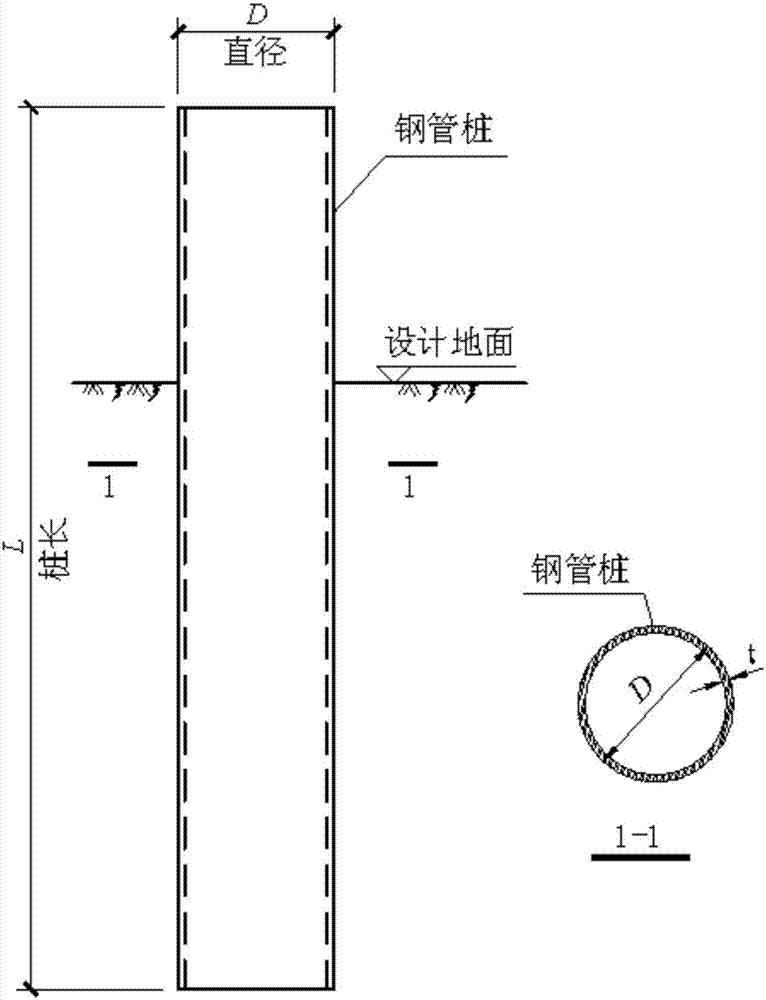
:目前全球范围内的海上风电机组基础常用基础形式主要有单桩基础、三脚架、导管架、重力式、吸力筒、漂浮式、以及高桩承台等基础形式;桩基础是海上风电基础最主要的应用形式,其中单桩基础的应用约占所有基础类型的60%左右。我国目前海上风电基础也以大直径单桩基础为主,通常采用直径3m~7m的单根钢管桩作为风力发电机的基础。目前,海上风电场工程中的钢管桩基础均为管状结构(详见图1)。风电机组单桩基础除承受重力荷载之外,还承受风、浪、流等水平荷载作用,在设计中需要重点考虑其水平承载性能;桩的直径往往由水平承载能力控制。桩的水平承载能力由桩的直径、桩身抗弯能力及桩侧土抗力所控制,而桩侧土抗力的大部分由地表附近的土层提供。所以要增大桩的水平向承载能力,一个办法是增大桩身直径;另一个办法是在地表附近土层的桩身周围增加径向翼,构成径向加翼钢管桩(详见图2)。在桩身水平承载能力相同的前提下,只要设计合理,采用“径向加翼钢管桩”往往比“增大桩身直径”具有更好的经济性。针对径向加翼大直径钢管桩,为找到合理的翼板设计参数,特进行相关研究,从“安全、经济、实用”的原则出发,发明了一种“径向小高度加翼大直径钢管桩”,并给出了其水平承载力的计算方法。技术实现要素:目的:为了克服现有技术中存在的不足,本发明提供一种径向小高度加翼大直径钢管桩及其水平承载力计算方法。技术方案:为解决上述技术问题,本发明采用的技术方案为:一种径向小高度加翼大直径钢管桩及其水平承载力计算方法,包括如下步骤:步骤一:针对钢管直径d=3m~7.5m、无径向翼的普通弹性长桩,先根据《建筑桩基技术规范》jgj94-2008计算其水平承载力特征值的“基础值”rh0;步骤二:针对钢管直径d=3m~7.5m、无径向翼的普通弹性长桩,采用数值分析手段,计算其水平承载能力rh1,以及地面处桩身的水平位移y1;然后以步骤一中的rh0为基础,通过回归分析,得到不同直径钢管桩水平承载力的“尺寸效应系数”kd,即:kd=rh1/rh0=(0.25lnd+0.86);步骤三:针对钢管直径d=3m~7.5m、设置径向翼的弹性长桩,利用ansys软件建立桩、径向翼和地基土在桩顶水平荷载作用下的整体数值模型;采用数值分析手段,分析不同径向翼数量n、不同翼板高度hs、不同径向翼长度ls条件下的桩在桩顶水平荷载h作用下,地面处桩身的水平位移y2,其中取ds=0m;步骤四:针对步骤三中的计算结果,按照“地面处桩身的水平位移与桩顶水平荷载成正比”的原则,通过优化分析,结合海上风电基础大直径钢管桩的施工特点,确定径向翼的高度hs;经过对比分析,确定本发明中的翼板高度hs=0.3m~0.5m;步骤五:以步骤二中的y1为基础,对步骤三~步骤四中的计算结果进行回归分析,找出径向加翼钢管桩水平承载能力的“翼板效应系数”ks,即:ks=y1/y2;步骤六:根据步骤一~步骤五,可以得到径向小高度加翼,hs=0.3m~0.5m大直径钢管桩的水平承载力rha=kskdrh0;即:rha=[1+(0.01n+0.10)ls0.2](0.97+0.1hs)(6/d)0.076(0.25lnd+0.86)×rh0。有益效果:本发明提供的径向小高度加翼大直径钢管桩及其水平承载力计算方法,通过合理设置径向翼,可以使大直径钢管桩中“较小直径径向加翼钢管桩”与“较大直径普通钢管桩”具有相同的水平承载能力;在满足水平承载能力要求的前提下,可以减少钢管桩基础的用钢量。当翼板数量取6~8个、翼板高度取0.3m~0.5m、翼板长度取5m~10m、翼板顶部位于设计地面(设计泥面)处时,在水平承载能力相同的前提下,相比非加翼的d=4.0m、5.0m、6.0m、7.0m大直径普通钢管桩(入土深度按40m计),“径向小高度加翼大直径钢管桩”分别节约钢材可达20t、30t、42t、55t,钢材用量节约10%~12%;仅每根桩的材料费和加工费就可节省投资约10万元、15万元、21万元、27万元,经济效益较为显著。因此,将本发明用于海上风电场风电机组大直径钢管桩单桩基础工程,可以获得良好的经济效益和社会效益。附图说明图1为普通钢管桩结构示意图;图2为径向小高度加翼大直径钢管桩结构示意图;图3为a-a方向的剖视图;图4为b-b方向的剖视图。具体实施方式下面结合附图对本发明作更进一步的说明。如图2、3、4所示,一种径向小高度加翼大直径钢管桩,钢管桩1侧壁上均匀设置有多个径向翼2,d为钢管桩1的外径;t为钢管桩1的钢管壁厚。径向翼2的数量n:n≥4,一般为6~8个。径向翼2的高度hs:径向翼的高度根据水平承载能力的要求,通过计算加以确定;为保证钢管桩受力特性的对称性,方便施工,各个翼的高度取相同的值。径向翼2的长度ls:径向翼的长度根据水平承载能力的要求,通过计算加以确定;为保证钢管桩受力特性的对称性,方便施工,各个翼的长度取相同的值。径向翼2的厚度ts:径向翼的厚度根据水平承载能力的要求,通过计算加以确定;为保证钢管桩受力特性的对称性,方便施工,各个翼的厚度取相同的值。径向翼2顶部到设计地面(最大冲刷线)的距离ds:为防止径向翼露出地面(海床面)加剧桩周围的局部冲刷,径向翼应埋设在设计地面(最大冲刷线)以下;但为了充分发挥径向翼的作用,埋置深度不宜过大;一般情况下,可取ds=0m。径向翼2的布置:径向翼和钢管桩的管身应可靠连接,以保证钢管桩的受力特性满足要求。为了保证钢管桩的受力性能,便于钢管桩的打设,径向翼的长度方向和钢管桩的桩身长度方向保持一致;为保证钢管桩受力特性的对称性,径向翼沿钢管桩周长等间距布置。一种径向小高度加翼大直径钢管桩水平承载力计算方法,包括步骤如下:步骤一:针对钢管直径d=3m~7.5m、无径向翼的普通弹性长桩,先根据《建筑桩基技术规范》jgj94-2008计算其水平承载力特征值的“基础值”rh0;步骤二:针对钢管直径d=3m~7.5m、无径向翼的普通弹性长桩,采用数值分析手段,计算其水平承载能力rh1,以及地面处桩身的水平位移y1;然后以步骤一中的rh0为基础,通过回归分析,得到不同直径钢管桩水平承载力的“尺寸效应系数”kd,即:kd=rh1/rh0=(0.25lnd+0.86);具体过程如下:步骤201:针对钢管直径d=3m、4m、5m、6m、7.5m的无径向翼的普通弹性长桩,利用ansys软件建立桩和地基土在桩顶水平荷载作用下的整体数值模型;数值模型中:桩顶高出地面为15m,水平荷载作用在桩顶;桩入土深度≥弹性长桩的入土深度,本处取40m;桩身壁厚取0.01d,采用shell181壳体单元模拟;桩平面位置位于地基土体模型范围的中间;地基土体模型范围取60m(长)×60m(宽)×64m(深),地基土体采用solid185实体单元模拟;在土体侧面的所有节点施加法向位移约束,在土体底部节点采用固定端约束;考虑桩侧面和土之间的竖向摩擦力效应;在土体中桩与土体之间的接触采用面面接触的形式,接触单元桩体采用targel70单元、土体采用contal74单元;桩外侧土体与桩外表面设置接触对,桩内土体与桩体的接触面同样设置接触对;接触算法采用罚函数形式;步骤202:对所述直径d中每种钢管桩,利用整体数值模型,计算其在桩顶水平荷载h作用下、地面处桩身的水平位移y1;步骤203:对步骤202中同一规格钢管桩,根据《建筑桩基技术规范》jgj94-2008,计算其在桩顶水平荷载h作用下、地面处桩身的水平位移y0;步骤204:令地面处桩身的水平位移与桩顶水平荷载成正比,则对同一规格的钢管桩,考虑桩和土之间的竖向摩擦力效应后,其水平承载力“尺寸效应系数”kd为:kd=y0/y1;步骤205:对不同桩径、不同土层分布的多个算例进行分析,可以得到各直径钢管桩“尺寸效应系数”kd的统计值,见表1:表1钢管桩“尺寸效应系数”kd一览表钢管桩直径d(m)34567.5“尺寸效应系数”kd1.121.231.281.321.35对表1中的数据进行回归分析,可得kd与d之间的关系式,见下:kd=(0.25lnd+0.86),其相关系数的平方r2=0.96。步骤三:针对钢管直径d=3m~7.5m、设置径向翼的弹性长桩,利用ansys软件建立桩、径向翼和地基土在桩顶水平荷载作用下的整体数值模型;数值模型中:桩顶高出地面为15m,水平荷载作用在桩顶;桩入土深度≥弹性长桩的入土深度,本处取40m;桩身壁厚取0.01d,径向翼厚度ts=0.01hs,桩身及径向翼采用shell181壳体单元模拟;桩平面位置位于地基土体模型范围的中间;地基土体模型范围取60m(长)×60m(宽)×64m(深),地基土体采用solid185实体单元模拟;在土体侧面的所有节点施加法向位移约束,在土体底部节点采用固定端约束;考虑桩侧面、径向翼侧面和土之间的竖向摩擦力效应;在土体中桩或径向翼与土体之间的接触采用面面接触的形式,接触单元桩体或径向翼采用targel70单元、土体采用contal74单元;桩外侧土体与桩外表面及径向翼表面设置接触对,桩内土体与桩体的接触面同样设置接触对;接触算法采用罚函数形式;采用数值分析手段,分析不同径向翼数量n、不同翼板高度hs、不同径向翼长度ls条件下的桩在桩顶水平荷载h作用下,地面处桩身的水平位移y2,其中取ds=0m;步骤四:针对步骤三中的计算结果,按照“地面处桩身的水平位移与桩顶水平荷载成正比”的原则,通过优化分析,结合海上风电基础大直径钢管桩的施工特点,确定径向翼的高度hs;经过对比分析,确定本发明中的翼板高度hs=0.3m~0.5m;具体过程如下:步骤401:以d=6.0m钢管桩(弹性长桩)为基准,分别取径向翼数量n=4、6、8,径向翼高度hs=0.3m、0.5m、0.7m、1.0m,径向翼长度ls=5m、10m、15m,建立相应的数值模型(参见步骤三),计算不同参数组合的钢管桩在桩顶水平荷载h作用下、地面处桩身的水平位移y2;同时建立d=6.0m无翼板钢管桩相应的数值模型(参见步骤201),计算其在桩顶水平荷载h作用下、地面处桩身的水平位移y1;数值模型中,均考虑桩侧面和土之间的竖向摩擦力效应;步骤402:令地面处桩身的水平位移与桩顶水平荷载成正比,以d=6.0m无径向翼钢管桩的水平承载力为基准,计算d=6.0m加翼钢管桩的水平承载力增大系数ks,6:ks,6=y1/y2,结果见表2:表2d=6.0m加翼钢管桩水平承载力增大系数ks,6一览表步骤403:选择ks,6最优的组合,从表2可看出:对加翼钢管桩,随着翼板数量n的增加、翼板长度ls的增大,其水平承载能力相应增大;随着翼板高度hs的增加,受桩身强度及翼板强度的影响,其水平承载能力先增加、后趋于稳定,翼板高度hs在0.30m~0.50m之间时,其综合经济性较好;考虑到海上大直径钢管桩的运输问题,为减小因翼板高度过大而带来的运输难度,确定加翼钢管桩的翼板高度hs取0.30m~0.50m。步骤五:以步骤二中的y1为基础,对步骤三~步骤四中的计算结果进行回归分析,找出径向加翼钢管桩水平承载能力的“翼板效应系数”ks,即:ks=y1/y2;具体过程如下:步骤501:对表2中hs=0.30m、0.50m的ks,6进行回归分析,可以得到d=6.0m、n∈[4,8]、ls∈[5m,15m]、hs∈[0.3m,0.5m]的加翼钢管桩的“翼板效应系数”ks(n,ls,hs,d=6m)的计算公式,见下式:ks(n,ls,hs,d=6m)=[1+(0.01n+0.10)ls0.2](0.97+0.1hs);步骤502:对其他直径的加翼钢管桩,令其“翼板效应系数”ks(n,ls,hs,d)与ks(n,ls,hs,d=6m)之间存在如下关系:ks(n,ls,hs,d)=ks(n,ls,hs,d=6m)×ks(d),并且对不同的n、ls、hs组合,ks(d)具有相同的计算公式;步骤503:分别取d=3.0m、4.0m、5.0m、6.0m、7.0m;对每一个直径的钢管桩(弹性长桩),取径向翼数量n=4,径向翼高度hs=0.3m,径向翼长度ls=5m,建立相应的数值模型(参见步骤三),计算不同直径加翼钢管桩在桩顶水平荷载h作用下、地面处桩身的水平位移y2,d;数值模型中,考虑桩侧面和土之间的竖向摩擦力效应;步骤504:对步骤503中d=3.0m、4.0m、5.0m、6.0m、7.0m的无翼板钢管桩,建立相应的数值模型(参见步骤二),计算不同直径钢管桩在桩顶水平荷载h作用下、地面处桩身的水平位移y1,d;数值模型中,考虑桩和土之间的竖向摩擦力效应;步骤505:令地面处桩身的水平位移与桩顶水平荷载成正比;根据步骤503、步骤504中的计算结果,可得到n=4、hs=0.3m、ls=5m的相应直径钢管桩的“翼板效应系数”ks(n=4,hs=0.3m,ls=5m,d):ks=y1,d/y2,d,结果见表3:表3n=4、hs=0.3m、ls=5m时不同直径钢管桩ks一览表钢管桩直径d(m)34567ks1.261.221.201.191.18对表3中的数据进行回归分析,可得ks(n=4,hs=0.3m,ls=5m,d)与d之间的关系式,见下:ks(n=4,hs=0.3m,ls=5m,d)=1.361d-0.076,其相关系数的平方r2=0.97;步骤506:根据步骤502可得:ks(d)=ks(n=4,hs=0.3m,ls=5m,d)/ks(n=4,hs=0.3m,ls=5m,d=6m);将步骤505中ks(n=4,hs=0.3m,ls=5m,d)=1.361d-0.076带入上式,可得:k(d)=(6/d)0.076;从而可得:ks=ks(n,ls,hsd)=[1+(0.01n+0.10)ls0.2](0.97+0.1hs)(6/d)0.076;式中n为径向翼数量,n∈[4,8];ls为径向翼长度,以m计,ls∈[5m,15m];hs为径向翼高度,以m计,hs∈[0.3m,0.5m];d为钢管桩外直径,以m计,d∈[3m,7.5m];步骤六:根据步骤一~步骤五,可以得到径向小高度加翼(hs=0.3m~0.5m)大直径钢管桩的水平承载力rha=kskdrh0;即:rha=[1+(0.01n+0.10)ls0.2](0.97+0.1hs)(6/d)0.076(0.25lnd+0.86)×rh0;式中相关参数的意义见步骤一~步骤五。以下举例说明本发明在工程中的应用及其经济效益。对泥质海域处的风电场,如果风电机组基础采用大直径钢管桩单桩基础,桩身壁厚t可取管桩外径d的1%左右,桩身强度即可满足要求;一般情况下,钢管桩基础的水平承载能力由地基土的强度控制,其控制指标体现在泥面处桩身水平位移上。为便于分析,下文取钢管桩的壁厚t≈0.01d,其中包含预留腐蚀厚度δt,一般取δt=3mm~5mm。例1:普通钢管桩桩径d=4.0m,设计壁厚t=42mm,预留腐蚀厚度δt=3mm,则计算壁厚为39mm;钢材的弹性模量e=2.0×105mpa;桩入土深度lh=40m(为弹性长桩),设计地面(泥面)以上的长度(即桩顶到设计地面的长度)lx=20m;按照《建筑桩基技术规范》jgj94-2008,地基土的m值为4.0mn/m4(未考虑桩径的尺寸效应)。等效水平荷载作用在桩顶,泥面处桩身水平位移允许值[y0]=20mm。取加翼钢管桩的lh、lx与普通钢管桩相同;求水平承载能力与该普通钢管桩等效的加翼钢管桩设计参数,并分析加翼钢管桩的经济效益。根据《建筑桩基技术规范》jgj94-2008,该钢管桩的水平承载能力rh0按下式计算:式中:b0=0.9(d+1),以米计;i为桩横截面惯性矩。经计算,α=0.157,rh0=1945kn;桩尺寸效应系数kd=(0.25lnd+0.86)=1.207;则该桩的水平承载能力rha=kdrh0=2347kn。加翼钢管桩的水平承载能力按本发明给出的公式计算:rha=[1+(0.01n+0.10)ls0.2](0.97+0.1hs)(6/d)0.076(0.25lnd+0.86)×rh0;其中的rh0根据加翼钢管桩的桩径、壁厚等参数,按照《建筑桩基技术规范》jgj94-2008进行计算。令普通钢管桩的水平承载能力与加翼钢管桩的水平承载能力相等,即可求出加翼钢管桩的相关设计参数;对加翼钢管桩翼板厚度ts,从翼板的强度、刚度及稳定方面考虑,取ts=0.1hs。加翼钢管桩的经济效益以其节约的钢材用量表征。实际工程中,设计地面以上的桩径可以根据风机的安装要求加以调整,不一定与入土段桩取同样的直径;为方便起见,可认为两种钢管桩设计地面以上部分的结构形式相同,不参与经济比较;只比较设计地面以下段钢管桩的用钢量。加翼钢管桩设计参数及其经济效益计算结果见表4所示。表4加翼钢管桩设计参数及其经济效益一览表(相比d=4.0m普通钢管桩)分别取普通钢管桩桩径d=5.0m、设计壁厚t=52mm,d=6.0m、设计壁厚t=62mm,桩径d=7.0m、设计壁厚t=72mm;其他参数与例1中的参数相同。求水平承载能力与相应直径普通钢管桩等效的加翼钢管桩设计参数,并分析加翼钢管桩的经济效益。按照例1的方法进行计算,则同样可得加翼钢管桩设计参数及其经济效益;结果见表5~表7所示。表5加翼钢管桩设计参数及其经济效益一览表(相比d=5.0m普通钢管桩)表6加翼钢管桩设计参数及其经济效益一览表(相比d=6.0m普通钢管桩)表7加翼钢管桩设计参数及其经济效益一览表(相比d=7.0m普通钢管桩)从表4~表7可看出:“径向小高度加翼大直径钢管桩”具有良好的经济效益;当翼板数量取6~8个、翼板高度取0.3m~0.5m、翼板长度取5m~10m时,在水平承载能力相同的前提下,相比非加翼的d=4.0m、5.0m、6.0m、7.0m大直径普通钢管桩,“径向小高度加翼大直径钢管桩”分别节约钢材约20t、30t、42t、55t,钢材用量节约10%~12%;仅每根桩的材料费和加工费就可节省投资约10万元、15万元、21万元、27万元,经济效益较为显著。以上所述仅是本发明的优选实施方式,应当指出:对于本
技术领域:
的普通技术人员来说,在不脱离本发明原理的前提下,还可以做出若干改进和润饰,这些改进和润饰也应视为本发明的保护范围。当前第1页12
相关技术
网友询问留言
已有0条留言
- 还没有人留言评论。精彩留言会获得点赞!
1